application homework problem

Solve step-by-step with MathGPT

Get instant homework help from your personal ai math solver.

Click here to take a picture or select an image

Drag & drop or click here to upload an image or PDF

Login Get started

Math Review of Solving Application Problems

• July 24, 2014
• No Comments

Solving application problems is a process that includes understanding the problem, translating it into an equation, solving the equation, checking the answer, and answering the question. This process can be used to solve many different types of problems.

Understanding and Setting up The Application Problem

The first part of the process involves understanding what is being asked. This includes noticing any key words that refer to operations and any quantities that are in relationship to one another. It is important to have an idea of what sort of quantity will represent a solution. Suppose a problem asks how many points the first-place winner had. That would require just one answer. If the problem described that the first-place winner had 10 points more than the second-place winner, and 17 points more than the third-place winner, all three point values would be necessary to completely answer the question.

Figure 1: Setting up the application problem involves finding quantities in relationship to one another.

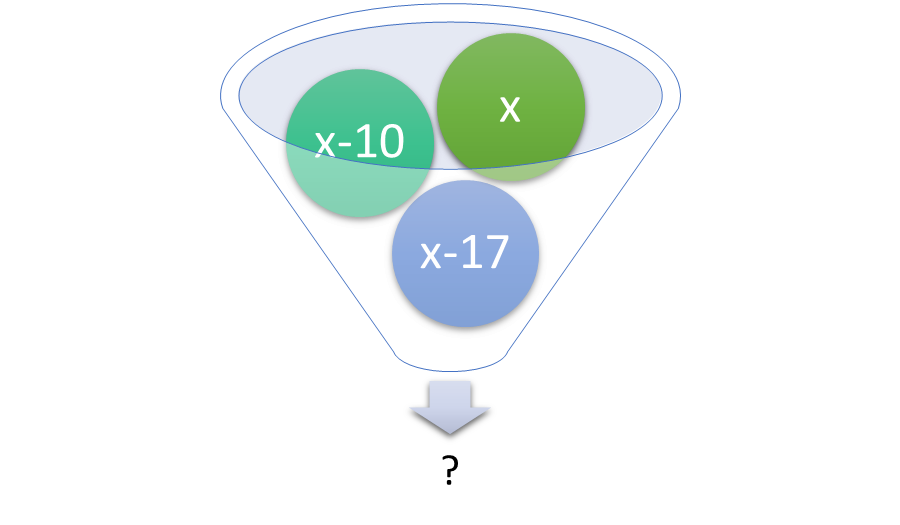
Translating the Problem into an Equation

The second part of the problem involves putting the problem in symbol form. This includes choosing a letter to represent a variable, and writing down exactly what the variable stands for. Suppose that the point values of the three winners totaled 114. Let the point value of the first-place winner be x, the second-place winner x – 10, and the third-place winner x – 17. Then, x + x – 10 + x – 17 = 114.

Figure 2: Translating the problem into an equation involves putting the problem into symbol form.

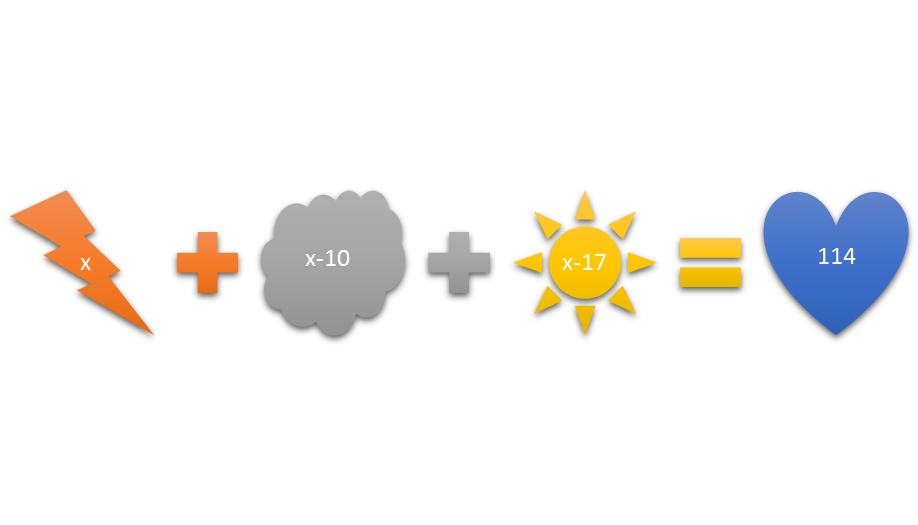
Solving and Checking the Equation

If x + x – 10 + x – 17 = 114, then 3x = 114 + 27, or 3x = 141. So, x = 47, x – 10 = 37, and x -17 = 30. To check, 47 + 37 + 30 = 114. The answer makes sense, and fits the parameters of the problem. In this case, the original equation was x + x -10 + x – 17 = 114.

Answer the Question Asked

If the work is done to understand the problem before it is set up and solved, it is easier to answer the appropriate question. In this case, all three point values were necessary to completely answer the question. Suppose that more information were added to the problem. During the same contest last year, the point values of the first-place, second-place and third-place winners totaled 100, but the second place winner had 14 points less than the first-place winner, and the third-place winner had 18 points less than the first place winner. Which year did the third-place winner earn more points, and what was the difference? Last year, the equation was x + x – 14 + x – 18 = 100, so 3x = 132. The first-place winner earned 44 points, the second-place winner earned 44-14 or 30 points, and the third-place winner earned 28 points. However, the question asked has 2 parts. Last year, the third-place winner earned 28 points, and this year, the third-place winner earned 30 points. This year, the third-place winner earned more points, and the difference was a gain of 2 points.

Figure 3: Answering the question asked brings all the parts of the problem into balance.

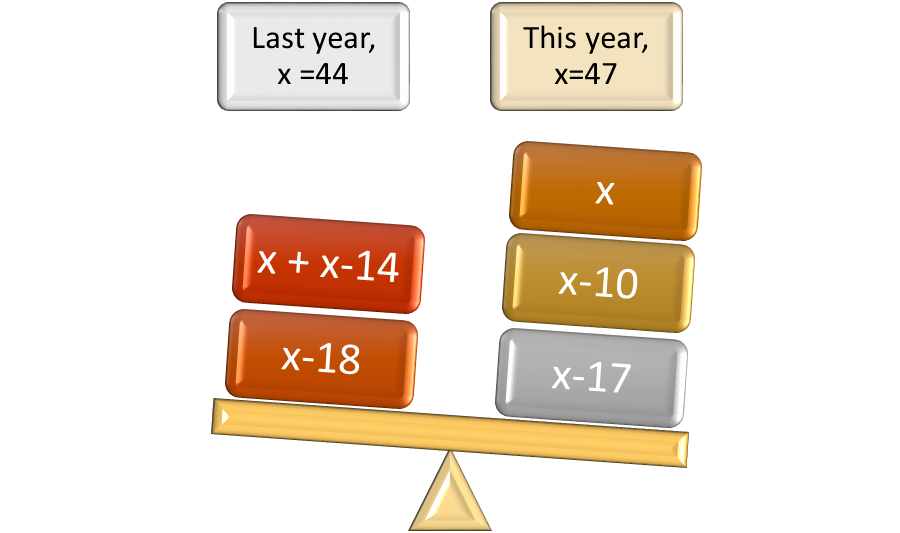
Interested in algebra tutoring services ? Learn more about how we are assisting thousands of students each academic year.

SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Lenexa, KS: visit Tutoring in Lenexa, KS

Math Review of Changing Application Problems into Equations

Math review of factoring a monomial from a polynomial.

StudyMonkey

Your personal ai tutor.

Learn Smarter, Not Harder with AI

Introducing StudyMonkey, your AI-powered tutor .

StudyMonkey AI can tutor complex homework questions, enhance your essay writing and assess your work—all in seconds.

No more long all-nighters

24/7 solutions to questions you're stumped on and essays you procrastinated on.

No more stress and anxiety

Get all your assignments done with helpful answers in 10 seconds or less.

No more asking friends for help

StudyMonkey is your new smart bestie that will never ghost you.

No more staying after school

AI tutoring is available 24/7, on-demand when you need it most.

AI Tutor for any subject

American college testing (act), anthropology, advanced placement exams (ap exams), arabic language, archaeology, biochemistry, chartered financial analyst (cfa) exam, communications, computer science, certified public accountant (cpa) exam, cultural studies, cyber security, dental admission test (dat), discrete mathematics, earth science, elementary school, entrepreneurship, environmental science, essay writer, farsi (persian) language, fundamentals of engineering (fe) exam, gender studies, graduate management admission test (gmat), graduate record examination (gre), greek language, hebrew language, high school entrance exam, high school, human geography, human resources, international english language testing system (ielts), information technology, international relations, independent school entrance exam (isee), lesson planner, linear algebra, linguistics, law school admission test (lsat), machine learning, master's degree, medical college admission test (mcat), meteorology, microbiology, middle school, national council licensure examination (nclex), national merit scholarship qualifying test (nmsqt), number theory, organic chemistry, project management professional (pmp), political science, portuguese language, probability, project management, preliminary sat (psat), public policy, public relations, russian language, scholastic assessment test (sat), social sciences, secondary school admission test (ssat), sustainability, swahili language, test of english as a foreign language (toefl), trigonometry, turkish language, united states medical licensing examination (usmle), web development, step-by-step guidance 24/7.

Receive step-by-step guidance & homework help for any homework problem & any subject 24/7

Ask any question

StudyMonkey supports every subject and every level of education from 1st grade to masters level.

Get an answer

StudyMonkey will give you an answer in seconds—multiple choice questions, short answers, and even an essays are supported!

Review your history

See your past questions and answers so you can review for tests and improve your grades.

Try StudyMonkey for free

It's not cheating....

Try the AI homework helper for free and upgrade at your convenience

You're just learning smarter than everyone else

How Can StudyMonkey Help You?

Hear From Our Happy Students

"The AI tutor is available 24/7, making it a convenient and accessible resource for students who need help with their homework at any time."

"Overall, StudyMonkey is an excellent tool for students looking to improve their understanding of homework topics and boost their academic success."

Upgrade to StudyMonkey Premium!

Why not upgrade to StudyMonkey Premium and get access to all features?

• Practice Problems
• Assignment Problems
• Show all Solutions/Steps/ etc.
• Hide all Solutions/Steps/ etc.
• Solving Logarithm Equations
• Systems of Equations Introduction
• Polynomial Functions
• Systems of Equations
• Calculus II
• Calculus III
• Differential Equations
• Algebra & Trig Review
• Common Math Errors
• Complex Number Primer
• How To Study Math
• Cheat Sheets & Tables
• MathJax Help and Configuration
• Notes Downloads
• Complete Book
• Practice Problems Downloads
• Complete Book - Problems Only
• Complete Book - Solutions
• Assignment Problems Downloads
• Other Items
• Get URL's for Download Items
• Print Page in Current Form (Default)
• Show all Solutions/Steps and Print Page
• Hide all Solutions/Steps and Print Page

Section 6.5 : Applications

• continuously
• Determine the exponential growth equation for this population.
• How long will it take for the population to grow from its initial population of 250 to a population of 2000?
• Determine the exponential decay equation for this element.
• How long will it take for half of the element to decay?
• How long will it take until there is only 1 gram of the element left?

EMBARC.Online

Application problems.

A huge THANK YOU to Daniel Kaufmann who created the Google Slides.

I put the K-5 @eureka_math Application Problems on gSlides presentations. https://t.co/2ds2pzyZvQ Maybe use them for a 'Do Now' as Ss get settled in. Let me know if you find any errors. @dhabecker #elemmathchat — Daniel Kaufmann (@KauDan721) July 11, 2018

4.2 Solve Applications with Systems of Equations

Learning objectives.

By the end of this section, you will be able to:

• Solve direct translation applications
• Solve geometry applications

Solve uniform motion applications

Be prepared 4.4.

Before you get started, take this readiness quiz.

The sum of twice a number and nine is 31. Find the number. If you missed this problem, review Example 2.15 .

Be Prepared 4.5

Twins Jon and Ron together earned $96,000 last year. Ron earned $8000 more than three times what Jon earned. How much did each of the twins earn? If you missed this problem, review Example 2.19 .

Be Prepared 4.6

An express train and a local train leave Pittsburgh to travel to Washington, D.C. The express train can make the trip in four hours and the local train takes five hours for the trip. The speed of the express train is 12 miles per hour faster than the speed of the local train. Find the speed of both trains. If you missed this problem, review Example 2.43 .

Solve Direct Translation Applications

Systems of linear equations are very useful for solving applications. Some people find setting up word problems with two variables easier than setting them up with just one variable. To solve an application, we’ll first translate the words into a system of linear equations. Then we will decide the most convenient method to use, and then solve the system.

Solve applications with systems of equations.

• Step 1. Read the problem. Make sure all the words and ideas are understood.
• Step 2. Identify what we are looking for.
• Step 3. Name what we are looking for. Choose variables to represent those quantities.
• Step 4. Translate into a system of equations.
• Step 5. Solve the system of equations using good algebra techniques.
• Step 6. Check the answer in the problem and make sure it makes sense.
• Step 7. Answer the question with a complete sentence.

We solved number problems with one variable earlier. Let’s see how differently it works using two variables.

Example 4.14

The sum of two numbers is zero. One number is nine less than the other. Find the numbers.

Try It 4.27

The sum of two numbers is 10. One number is 4 less than the other. Find the numbers.

Try It 4.28

The sum of two numbers is −6 . −6 . One number is 10 less than the other. Find the numbers.

Example 4.15

Heather has been offered two options for her salary as a trainer at the gym. Option A would pay her $25,000 plus $15 for each training session. Option B would pay her $ 10,000 + $ 40 $ 10,000 + $ 40 for each training session. How many training sessions would make the salary options equal?

Try It 4.29

Geraldine has been offered positions by two insurance companies. The first company pays a salary of $12,000 plus a commission of $100 for each policy sold. The second pays a salary of $20,000 plus a commission of $50 for each policy sold. How many policies would need to be sold to make the total pay the same?

Try It 4.30

Kenneth currently sells suits for company A at a salary of $22,000 plus a $10 commission for each suit sold. Company B offers him a position with a salary of $28,000 plus a $4 commission for each suit sold. How many suits would Kenneth need to sell for the options to be equal?

As you solve each application, remember to analyze which method of solving the system of equations would be most convenient.

Example 4.16

Translate to a system of equations and then solve:

When Jenna spent 10 minutes on the elliptical trainer and then did circuit training for 20 minutes, her fitness app says she burned 278 calories. When she spent 20 minutes on the elliptical trainer and 30 minutes circuit training she burned 473 calories. How many calories does she burn for each minute on the elliptical trainer? How many calories for each minute of circuit training?

Try It 4.31

Mark went to the gym and did 40 minutes of Bikram hot yoga and 10 minutes of jumping jacks. He burned 510 calories. The next time he went to the gym, he did 30 minutes of Bikram hot yoga and 20 minutes of jumping jacks burning 470 calories. How many calories were burned for each minute of yoga? How many calories were burned for each minute of jumping jacks?

Try It 4.32

Erin spent 30 minutes on the rowing machine and 20 minutes lifting weights at the gym and burned 430 calories. During her next visit to the gym she spent 50 minutes on the rowing machine and 10 minutes lifting weights and burned 600 calories. How many calories did she burn for each minutes on the rowing machine? How many calories did she burn for each minute of weight lifting?

Solve Geometry Applications

We will now solve geometry applications using systems of linear equations. We will need to add complementary angles and supplementary angles to our list some properties of angles.

The measures of two complementary angles add to 90 degrees. The measures of two supplementary angles add to 180 degrees.

Complementary and Supplementary Angles

Two angles are complementary if the sum of the measures of their angles is 90 degrees.

Two angles are supplementary if the sum of the measures of their angles is 180 degrees.

If two angles are complementary, we say that one angle is the complement of the other.

If two angles are supplementary, we say that one angle is the supplement of the other.

Example 4.17

Translate to a system of equations and then solve.

The difference of two complementary angles is 26 degrees. Find the measures of the angles.

Try It 4.33

The difference of two complementary angles is 20 degrees. Find the measures of the angles.

Try It 4.34

The difference of two complementary angles is 80 degrees. Find the measures of the angles.

In the next example, we remember that the measures of supplementary angles add to 180.

Example 4.18

Two angles are supplementary. The measure of the larger angle is twelve degrees less than five times the measure of the smaller angle. Find the measures of both angles.

Try It 4.35

Two angles are supplementary. The measure of the larger angle is 12 degrees more than three times the smaller angle. Find the measures of the angles.

Try It 4.36

Two angles are supplementary. The measure of the larger angle is 18 less than twice the measure of the smaller angle. Find the measures of the angles.

Recall that the angles of a triangle add up to 180 degrees. A right triangle has one angle that is 90 degrees. What does that tell us about the other two angles? In the next example we will be finding the measures of the other two angles.

Example 4.19

The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle. Find the measures of both angles.

We will draw and label a figure.

Try It 4.37

The measure of one of the small angles of a right triangle is 2 more than 3 times the measure of the other small angle. Find the measure of both angles.

Try It 4.38

The measure of one of the small angles of a right triangle is 18 less than twice the measure of the other small angle. Find the measure of both angles.

Often it is helpful when solving geometry applications to draw a picture to visualize the situation.

Example 4.20

Randall has 125 feet of fencing to enclose the part of his backyard adjacent to his house. He will only need to fence around three sides, because the fourth side will be the wall of the house. He wants the length of the fenced yard (parallel to the house wall) to be 5 feet more than four times as long as the width. Find the length and the width.

Try It 4.39

Mario wants to put a fence around the pool in his backyard. Since one side is adjacent to the house, he will only need to fence three sides. There are two long sides and the one shorter side is parallel to the house. He needs 155 feet of fencing to enclose the pool. The length of the long side is 10 feet less than twice the width. Find the length and width of the pool area to be enclosed.

Try It 4.40

Alexis wants to build a rectangular dog run in her yard adjacent to her neighbor’s fence. She will use 136 feet of fencing to completely enclose the rectangular dog run. The length of the dog run along the neighbor’s fence will be 16 feet less than twice the width. Find the length and width of the dog run.

We used a table to organize the information in uniform motion problems when we introduced them earlier. We’ll continue using the table here. The basic equation was D = r t D = r t where D is the distance traveled, r is the rate, and t is the time.

Our first example of a uniform motion application will be for a situation similar to some we have already seen, but now we can use two variables and two equations.

Example 4.21

Joni left St. Louis on the interstate, driving west towards Denver at a speed of 65 miles per hour. Half an hour later, Kelly left St. Louis on the same route as Joni, driving 78 miles per hour. How long will it take Kelly to catch up to Joni?

A diagram is useful in helping us visualize the situation.

Identify and name what we are looking for. A chart will help us organize the data. We know the rates of both Joni and Kelly, and so we enter them in the chart. We are looking for the length of time Kelly, k , and Joni, j , will each drive.

Since D = r · t D = r · t we can fill in the Distance column.

Translate into a system of equations.

To make the system of equations, we must recognize that Kelly and Joni will drive the same distance. So,

Also, since Kelly left later, her time will be 1 2 1 2 hour less than Joni’s time. So,

Try It 4.41

Mitchell left Detroit on the interstate driving south towards Orlando at a speed of 60 miles per hour. Clark left Detroit 1 hour later traveling at a speed of 75 miles per hour, following the same route as Mitchell. How long will it take Clark to catch Mitchell?

Try It 4.42

Charlie left his mother’s house traveling at an average speed of 36 miles per hour. His sister Sally left 15 minutes ( 1 4 hour ) ( 1 4 hour ) later traveling the same route at an average speed of 42 miles per hour. How long before Sally catches up to Charlie?

Many real-world applications of uniform motion arise because of the effects of currents—of water or air—on the actual speed of a vehicle. Cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.

Let’s take a look at a boat travelling on a river. Depending on which way the boat is going, the current of the water is either slowing it down or speeding it up.

The images below show how a river current affects the speed at which a boat is actually travelling. We’ll call the speed of the boat in still water b and the speed of the river current c .

The boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat’s actual speed is faster than its speed in still water. The actual speed at which the boat is moving is b + c . b + c .

Now, the boat is going upstream, opposite to the river current. The current is going against the boat, so the boat’s actual speed is slower than its speed in still water. The actual speed of the boat is b − c . b − c .

We’ll put some numbers to this situation in the next example.

Example 4.22

A river cruise ship sailed 60 miles downstream for 4 hours and then took 5 hours sailing upstream to return to the dock. Find the speed of the ship in still water and the speed of the river current.

Try It 4.43

A Mississippi river boat cruise sailed 120 miles upstream for 12 hours and then took 10 hours to return to the dock. Find the speed of the river boat in still water and the speed of the river current.

Try It 4.44

Jason paddled his canoe 24 miles upstream for 4 hours. It took him 3 hours to paddle back. Find the speed of the canoe in still water and the speed of the river current.

Wind currents affect airplane speeds in the same way as water currents affect boat speeds. We’ll see this in the next example. A wind current in the same direction as the plane is flying is called a tailwind . A wind current blowing against the direction of the plane is called a headwind .

Example 4.23

A private jet can fly 1,095 miles in three hours with a tailwind but only 987 miles in three hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Try It 4.45

A small jet can fly 1,325 miles in 5 hours with a tailwind but only 1,035 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Try It 4.46

A commercial jet can fly 1,728 miles in 4 hours with a tailwind but only 1,536 miles in 4 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Access this online resource for additional instruction and practice with systems of equations.

• Systems of Equations

Section 4.2 Exercises

Practice makes perfect.

Direct Translation Applications

In the following exercises, translate to a system of equations and solve.

The sum of two number is 15. One number is 3 less than the other. Find the numbers.

The sum of two number is 30. One number is 4 less than the other. Find the numbers.

The sum of two number is −16. One number is 20 less than the other. Find the numbers.

The sum of two number is −26 . −26 . One number is 12 less than the other. Find the numbers.

The sum of two numbers is 65. Their difference is 25. Find the numbers.

The sum of two numbers is 37. Their difference is 9. Find the numbers.

The sum of two numbers is −27 . −27 . Their difference is −59 . −59 . Find the numbers.

The sum of two numbers is −45 . −45 . Their difference is −89 . −89 . Find the numbers.

Maxim has been offered positions by two car companies. The first company pays a salary of $10,000 plus a commission of $1000 for each car sold. The second pays a salary of $20,000 plus a commission of $500 for each car sold. How many cars would need to be sold to make the total pay the same?

Jackie has been offered positions by two cable companies. The first company pays a salary of $14,000 plus a commission of $100 for each cable package sold. The second pays a salary of $20,000 plus a commission of $25 for each cable package sold. How many cable packages would need to be sold to make the total pay the same?

Amara currently sells televisions for company A at a salary of $17,000 plus a $100 commission for each television she sells. Company B offers her a position with a salary of $29,000 plus a $20 commission for each television she sells. How many televisions would Amara need to sell for the options to be equal?

Mitchell currently sells stoves for company A at a salary of $12,000 plus a $150 commission for each stove he sells. Company B offers him a position with a salary of $24,000 plus a $50 commission for each stove he sells. How many stoves would Mitchell need to sell for the options to be equal?

Two containers of gasoline hold a total of fifty gallons. The big container can hold ten gallons less than twice the small container. How many gallons does each container hold?

June needs 48 gallons of punch for a party and has two different coolers to carry it in. The bigger cooler is five times as large as the smaller cooler. How many gallons can each cooler hold?

Shelly spent 10 minutes jogging and 20 minutes cycling and burned 300 calories. The next day, Shelly swapped times, doing 20 minutes of jogging and 10 minutes of cycling and burned the same number of calories. How many calories were burned for each minute of jogging and how many for each minute of cycling?

Drew burned 1800 calories Friday playing one hour of basketball and canoeing for two hours. Saturday he spent two hours playing basketball and three hours canoeing and burned 3200 calories. How many calories did he burn per hour when playing basketball? How many calories did he burn per hour when canoeing?

Troy and Lisa were shopping for school supplies. Each purchased different quantities of the same notebook and thumb drive. Troy bought four notebooks and five thumb drives for $116. Lisa bought two notebooks and three thumb dives for $68. Find the cost of each notebook and each thumb drive.

Nancy bought seven pounds of oranges and three pounds of bananas for $17. Her husband later bought three pounds of oranges and six pounds of bananas for $12. What was the cost per pound of the oranges and the bananas?

Andrea is buying some new shirts and sweaters. She is able to buy 3 shirts and 2 sweaters for $114 or she is able to buy 2 shirts and 4 sweaters for $164. How much does a shirt cost? How much does a sweater cost?

Peter is buying office supplies. He is able to buy 3 packages of paper and 4 staplers for $40 or he is able to buy 5 packages of paper and 6 staplers for $62. How much does a package of paper cost? How much does a stapler cost?

The total amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot dog? How much sodium is in a cup of cottage cheese?

The total number of calories in 2 hot dogs and 3 cups of cottage cheese is 960 calories. The total number of calories in 5 hot dogs and 2 cups of cottage cheese is 1190 calories. How many calories are in a hot dog? How many calories are in a cup of cottage cheese?

Molly is making strawberry infused water. For each ounce of strawberry juice, she uses three times as many ounces of water as juice. How many ounces of strawberry juice and how many ounces of water does she need to make 64 ounces of strawberry infused water?

Owen is making lemonade from concentrate. The number of quarts of water he needs is 4 times the number of quarts of concentrate. How many quarts of water and how many quarts of concentrate does Owen need to make 100 quarts of lemonade?

The difference of two complementary angles is 55 degrees. Find the measures of the angles.

The difference of two complementary angles is 17 degrees. Find the measures of the angles.

Two angles are complementary. The measure of the larger angle is twelve less than twice the measure of the smaller angle. Find the measures of both angles.

Two angles are complementary. The measure of the larger angle is ten more than four times the measure of the smaller angle. Find the measures of both angles.

The difference of two supplementary angles is 8 degrees. Find the measures of the angles.

The difference of two supplementary angles is 88 degrees. Find the measures of the angles.

Two angles are supplementary. The measure of the larger angle is four more than three times the measure of the smaller angle. Find the measures of both angles.

Two angles are supplementary. The measure of the larger angle is five less than four times the measure of the smaller angle. Find the measures of both angles.

The measure of one of the small angles of a right triangle is 14 more than 3 times the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 26 more than 3 times the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 15 less than twice the measure of the other small angle. Find the measure of both angles.

The measure of one of the small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles.

Wayne is hanging a string of lights 45 feet long around the three sides of his patio, which is adjacent to his house. The length of his patio, the side along the house, is five feet longer than twice its width. Find the length and width of the patio.

Darrin is hanging 200 feet of Christmas garland on the three sides of fencing that enclose his front yard. The length is five feet less than three times the width. Find the length and width of the fencing.

A frame around a family portrait has a perimeter of 90 inches. The length is fifteen less than twice the width. Find the length and width of the frame.

The perimeter of a toddler play area is 100 feet. The length is ten more than three times the width. Find the length and width of the play area.

Solve Uniform Motion Applications

Sarah left Minneapolis heading east on the interstate at a speed of 60 mph. Her sister followed her on the same route, leaving two hours later and driving at a rate of 70 mph. How long will it take for Sarah’s sister to catch up to Sarah?

College roommates John and David were driving home to the same town for the holidays. John drove 55 mph, and David, who left an hour later, drove 60 mph. How long will it take for David to catch up to John?

At the end of spring break, Lucy left the beach and drove back towards home, driving at a rate of 40 mph. Lucy’s friend left the beach for home 30 minutes (half an hour) later, and drove 50 mph. How long did it take Lucy’s friend to catch up to Lucy?

Felecia left her home to visit her daughter driving 45 mph. Her husband waited for the dog sitter to arrive and left home twenty minutes (1/3 hour) later. He drove 55 mph to catch up to Felecia. How long before he reaches her?

The Jones family took a 12-mile canoe ride down the Indian River in two hours. After lunch, the return trip back up the river took three hours. Find the rate of the canoe in still water and the rate of the current.

A motor boat travels 60 miles down a river in three hours but takes five hours to return upstream. Find the rate of the boat in still water and the rate of the current.

A motor boat traveled 18 miles down a river in two hours but going back upstream, it took 4.5 4.5 hours due to the current. Find the rate of the motor boat in still water and the rate of the current.

A river cruise boat sailed 80 miles down the Mississippi River for four hours. It took five hours to return. Find the rate of the cruise boat in still water and the rate of the current.

A small jet can fly 1072 miles in 4 hours with a tailwind but only 848 miles in 4 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

A small jet can fly 1435 miles in 5 hours with a tailwind but only 1,215 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

A commercial jet can fly 868 miles in 2 hours with a tailwind but only 792 miles in 2 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

A commercial jet can fly 1,320 miles in 3 hours with a tailwind but only 1170 miles in 3 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.

Writing Exercises

Write an application problem similar to Example 4.14 . Then translate to a system of equations and solve it.

Write a uniform motion problem similar to Example 4.15 that relates to where you live with your friends or family members. Then translate to a system of equations and solve it.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-2-solve-applications-with-systems-of-equations

© Jul 24, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.6: Application II - Solving Problems

• Last updated
• Save as PDF
• Page ID 49371

• Denny Burzynski & Wade Ellis, Jr.
• College of Southern Nevada via OpenStax CNX

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Solving Applied Problems

Let’s study some interesting problems that involve linear equations in one variable. In order to solve such problems, we apply the following five-step method:

Five-Step Method for Solving Word Problems

• Let \(x\) (or some other letter) represent the unknown quantity.
• Translate the words to mathematical symbols and form an equation.
• Solve this equation.

If the answer doesn’t check, you have either solved the equation incorrectly, or you have developed the wrong equation. Check your method of solution first. If the result does not check, reconsider your equation.

• Write the conclusion.

If it has been your experience that word problems are difficult, then follow the five-step method carefully. Most people have difficulty because they neglect step 1.

Always start by INTRODUCING A VARIABLE!

Keep in mind what the variable is representing throughout the problem.

Sample Set A

Example \(\pageindex{1}\).

This year an item costs $44, an increase of $3 over last year's price. What was last year's price?

\(\begin{array}{flushleft} \text{Step 1: }\text{Let }x&=&\text{last year's price}\\ \text{Step 2: }x+3&=&44&x+3\text{ represents the \$3 increase in price.}\\ \text{Step 3: }&x+3&=&44\\ &x+3-3&=&44-3\\ &x&=&41\\ \text{Step 4: }&41+3&=&44&\text{Yes, this is correct}\\ \text{Step 5: Last year's price was \$41}. \end{array}\)

Practice Set A

Practice problem \(\pageindex{1}\).

This year an item costs $23, an increase of $4 over last year’s price. What was last year’s price?

• Last year's price was .

Last year's price was $19

Sample Set B

Example \(\pageindex{2}\).

The perimeter (length around) of a square is 60 cm (centimeters). Find the length of a side.

Step 1: Let \(x = \text{ length of a side.}\).

Step 2: We can draw a picture.

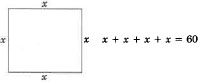
\(\begin{array}{flushleft} \text{Step 3: }&x+x+x+x&=&60\\ &4x&=&60&\text{Divide both sides by 4.}\\ &x&=&15\\ \text{Step 4: }&4(15)&=&60&\text{Yes, this is correct}\\ \text{Step 5: }&\text{The length of a side is 15 cm} \end{array}\)

Practice Set B

Practice problem \(\pageindex{2}\).

The perimeter of a triangle is 54 inches. If each side has the same length, find the length of a side.

• The length of a side is inches.

The length of a side is 18 inches.

Sample Set C

Six percent of a number is 54. What is the number?

\(\begin{array}{flushleft} \text{Step 1: }&\text{Let } x = \text{the number}\\ \text{Step 2: }&\text{We must convert 6% to a decimal}\\ \end{array}\) \(\begin{array}{flushleft} &6\%&=&.06\\ &.06x&=&54&.06x\text{ occurs because we want 6% of } x.\\ \text{Step 3: }&.06x&=&54&\text{Divide both sides by } .06.\\ &x&=&\dfrac{54}{.06}\\ &x&=&900\\ \text{Step 4: }&.06(900)&=&54.&\text{Yes, this is correct.}\\ \text{Step 5: }&\text{The number is } 900. \end{array}\)

Practice Set C

Practice problem \(\pageindex{3}\).

Eight percent of a number is 36. What is the number?

• The number is .

The number is 450.

Sample Set D

Example \(\pageindex{4}\).

An astronomer notices that one star gives off about 3.6 times as much energy as another star. Together the stars give off 55.844 units of energy. How many units of energy does each star emit?

1. In this problem we have two unknowns and, therefore, we might think, two variables. However, notice that the energy given off by one star is given in terms of the other star. So, rather than introducing two variables, we introduce only one. The other unknown(s) is expressed in terms of this one. (We might call this quantity the base quantity.)

Let \(x=\) number of units of energy given off by the less energetic star. Then, \(3.6x=\) number of units of energy given off by the more energetic star.

\(\begin{array}{flushleft} \text{Step 2: }&x+3.6x&=&55.844\\ \text{Step 3: }&x+3.6x&=&55.844\\ &4.6x&=&55.844&\text{Divide both sides by } 4.6 \text{. A calculator would be useful at this point.}\\ &x&=&\dfrac{55.844}{4.6}\\ &x&=&12.14&\text{The wording of the problem implies two numbers are needed }\\ &&&&\text{for a complete solution. We need the number of units of}\\ &&&&\text{energy for the other star.}\\ &3.6x&=&3.6(12.14)\\ &&=&43.704\\ \text{Step 4: }&12.14+43.704&=&55.844&\text{Yes, this is correct}. \end{array}\) \(\text{Step 5: One start gives off } 12.14 \text{ units of energy and the other star gives off } 43.704 \text{ units of energy}\)

Practice Set D

Practice problem \(\pageindex{4}\).

Garden A produces 5.8 times as many vegetables as garden B. Together the gardens produce 102 pounds of vegetables. How many pounds of vegetables does garden A produce?

• Let \(x =\)

Garden A produces 87 pounds of vegetables.

Sample Set E

Example \(\pageindex{5}\).

Two consecutive even numbers sum to 432. What are the two numbers?

\(\text{Step 1: Let } x= \text{ the smaller even number. Then } x+2= \text{ the next (consecutive) even number}\\ \text{since consecutive even numbers differ by } 2 \text{ (as do consecutive odd numbers) }\)

\(\begin{array}{flushleft} \text{Step 2: }&x+x+2&=&432\\ \text{Step 3: }&x+x+2&=&432\\ &2x+2&=&432\\ &2x&=&430\\ &x&=&215&\text{Also, since } x=215, x+2=217 \end{array}\)

\(\text{Step 4: }215+217=432, \text{ but } 215 \text{ and } 217 \text{ are odd numbers and we are looking for even numbers.}\\ \text{Upon checking our method of solution and reexamining our equation, we find no}\\ \text{mistakes.}\)

\(\text{Step 5: We must conclude that this problem has no solution. There are no two consecutive even numbers that sum to 432}\)

Practice Set E

Exercise \(\pageindex{1}\).

The sum of two consecutive even numbers is 498. What are the two numbers?

The two numbers are 248 and 250.

Solve the following problems. Note that some of the problems may seem to have no practical applications and may not seem very interesting. They, along with the other problems, will, however, help to develop your logic and problem-solving ability.

If eighteen is subtracted from some number the result is fifty-two. What is the number?

• The equation is
• (Solve the equation.)

Step 1: Let \(x =\) the unknown quantity. Step 2: The equation is \(x−18=52\). Step 3: (Solve the equation.) Add 18 to each side.   \(  x−18+18=52+18\\     x=70\) Step 4: (Check) \(70−18=52\); True. Step 5: The number is 70.

Exercise \(\PageIndex{2}\)

If nine more than twice a number is forty-six, what is the number?

• The number is.

Exercise \(\PageIndex{3}\)

If nine less than three eighths of a number is two and one fourth, what is the number?

Step 5: The number is 30.

Exercise \(\PageIndex{4}\)

Twenty percent of a number is 68. What is the number?

Exercise \(\PageIndex{5}\)

Eight more than a quantity is 37. What is the original quantity?

• The original quantity is .

Step 5: The original quantity is 29.

Exercise \(\PageIndex{6}\)

If a quantity plus 85% more of the quantity is 62.9, what is the original quantity?

• Let x= original quantity.
• The original quantity is.

Exercise \(\PageIndex{7}\)

A company must increase production by 12% over last year’s production. The new output will be 56 items. What was last year’s output?

• Last year’s output was items.

Step 5: Last year's output was 50 items.

Exercise \(\PageIndex{8}\)

A company has determined that it must increase production of a certain line of goods by \(1\dfrac{1}{2}\) times last year’s production. The new output will be 2885 items. What was last year’s output?

Exercise \(\PageIndex{9}\)

A proton is about 1837 times as heavy as an electron. If an electron weighs 2.68 units, how many units does a proton weigh?

• A proton weighs units.

Step 5: A proton weighs 4923.16 units.

Exercise \(\PageIndex{10}\)

Three consecutive integers sum to 36. What are they?

Step 5: The first integer is 11; second is 12; third is 13.

Exercise \(\PageIndex{11}\)

Neptune is about 30 times as far from the sun as is the Earth. If it takes light 8 minutes to travel from the sun to the Earth, how many minutes does it take to travel to Neptune?

• Light takes minutes to reach Neptune.

Exercise \(\PageIndex{12}\)

The radius of the sun is about 695,202 km (kilometers). That is about 109 times as big as the radius of the Earth. What is the radius of the earth?

• The radius of the earth is km.

Step 5: The radius of the earth is 6378 km.

Exercise \(\PageIndex{13}\)

Three consecutive even integers add up to 131. What are they?

Exercise \(\PageIndex{14}\)

The perimeter of a triangle is 105 cm. If each of the two legs is exactly twice the length of the base, how long is each leg?

• Let \(=\) Draw a picture.
• Each leg is cm long. The base is .

Exercise \(\PageIndex{15}\)

A lumber company has contracted to cut boards into two pieces so that one piece is three times the length of the other piece. If a board is 12 feet long, what is the length of each piece after cutting?

• The length of the shorter piece is feet, and the length of the longer piece is feet.

Step 5: The length of the shorter piece is 3 feet, and the length of the longer piece is 9 feet.

Exercise \(\PageIndex{16}\)

Two consecutive odd integers sum to 151. What are they?

Exercise \(\PageIndex{17}\)

A student doing a chemistry experiment has a beaker that contains 84 ml (milliliters) of an alcohol and water solution. Her lab directions tell her that there is 4.6 times as much water as alcohol in the solution. How many milliliters of alcohol are in the solution? How many milliliters of water?

• There are ml of alcohol in the solution. There are ml of water in the solution.

Exercise \(\PageIndex{18}\)

A statistician is collecting data to help him estimate the average income of accountants in California. He needs to collect 390 pieces of data and he is \(\dfrac{2}{3}\) done. How many pieces of data has the statistician collected?

• The statistician has collected pieces of data. Suppose the statistician is 4 pieces of data short of being \(\dfrac{2}{3}\) done. How many pieces of data has he collected?

Step 5: The statistician has collected 260 pieces of data.

Exercise \(\PageIndex{19}\)

A television commercial advertises that a certain type of battery will last, on the average, 20 hours longer than twice the life of another type of battery. If consumer tests show that the advertised battery lasts 725 hours, how many hours must the other type of battery last for the advertiser’s claim to be valid?

• The other type of battery must last hours for the advertiser’s claim to be valid.

Exercise \(\PageIndex{20}\)

A 1000-ml flask containing a chloride solution will fill 3 beakers of the same size with 210 ml of the solution left over. How many milliliters of the chloride solution will each beaker hold?

• Each beaker will hold ml of the chloride solution.

Step 5: Each beaker will hold \(263\dfrac{1}{3}\) ml of chloride solution.

Exercise \(\PageIndex{21}\)

A star burns \(\dfrac{2}{9}\) of its original mass then blows off \(\dfrac{3}{7}\) of the remaining mass as a planetary nebula. If the final mass is 3 units of mass, what was the original mass?

• The original mass was units of mass.

Exercise \(\PageIndex{22}\)

The sum of a number and sixteen is forty-two. What is the number?

Step 5: The unknown number is 26.

Exercise \(\PageIndex{23}\)

When eleven is subtracted from a number, the result is 85. What is the number?

Exercise \(\PageIndex{24}\)

Three times a number is divided by 6 and the result is 10.5. What is the number?

Step 5: The unknown number is 21.

Exercise \(\PageIndex{25}\)

When a number is multiplied by itself, the result is 144. What is the number?

Exercise \(\PageIndex{26}\)

A number is tripled, then increased by seven. The result is 48. What is the number?

Step 5: The unknown number is \(\dfrac{41}{3}\).

Exercise \(\PageIndex{27}\)

Eight times a number is decreased by three times the number, giving a difference of 22. What is the number?

Exercise \(\PageIndex{28}\)

One number is fifteen more than another number. The sum of the two numbers is 27. What are they?

Step 5: One unknown number is 6; the other is 21.

Exercise \(\PageIndex{29}\)

The length of a rectangle is 6 meters more than three times the width. The perimeter of the rectangle is 44 meters What are the dimensions of the rectangle?

Exercise \(\PageIndex{30}\)

Seven is added to the product of 41 and some number. The result, when divided by four, is 63. What is the number?

Step 5: The unknown number is \(\dfrac{245}{41}\).

Exercise \(\PageIndex{31}\)

The second side of a triangle is five times the length of the smallest side. The third is twice the length of the second side. The perimeter of the triangle is 48 inches. Find the length of each side.

Exercise \(\PageIndex{32}\)

Person A is four times as old as person B, who is six times as old as person C, who is twice as old as person D. How old is each person if their combined ages are 189 months?

Exercise \(\PageIndex{33}\)

As a consequence of Einstein’s theory of relativity, the rate of time passage is different for a person in a stationary position and a person in motion. (Hard to believe, but true!) To the moving observer, the rate of time passage is slower than that of the stationary observer, that is, the moving person ages slower than the stationary observer. (This fact has been proven many times by experiments with radioactive materials.) The effect is called “time dilation” and is really only noticeable when an object is traveling at near the speed of light (186,000 miles per second). Considering these ideas, try to solve the following problems:

Two people have identical clocks. One is standing on the earth and the other is moving in a spacecraft at 95% the speed of light, 176,700 miles per second. The moving person’s rate of time passage at this speed is about 0.31 times as fast as the person standing on earth.

• If two days of earth time pass, how many days actually pass on the spacecraft?
• years have passed on the spacecraft.
• If 30 years have passed on the spacecraft, how many years have passed on the earth?
• A space traveler makes a round-trip voyage to the star Capella. The trip takes her 120 years (traveling at 176,000 miles per second). If it is the year 2000 on earth when she leaves, what earth year will it be when she returns?

(a) Step 5: The time passed in space is 0.62 days. (b) Step 5: 9.3 years have passed on the spacecraft. (c) Step 5: 96.77 years have passed on the earth. (d) Step 5: Earth year when she returns will be 2387.

Exercises for Review

Exercise \(\pageindex{34}\).

Specify the domain of the equation \(y = \dfrac{x-1}{x+4}\)

Exercise \(\PageIndex{35}\)

Classify the equation \(x+4=1\) as an identity, a contradiction, or a conditional equation.

conditional

Exercise \(\PageIndex{36}\)

Classify the equation \(2x+3=2x+3\) as an identity, a contradiction or a conditional equation.

Exercise \(\PageIndex{37}\)

Solve the equation \(4(x−1)+12=−3(2x+4)\).

\(x=−2\)

Exercise \(\PageIndex{38}\)

Translate the following sentence to a mathematical equation. Three less than an unknown number is multiplied by negative four. The result is two more than the original unknown number.

• High School
• You don't have any recent items yet.
• You don't have any courses yet.
• You don't have any books yet.
• You don't have any Studylists yet.
• Information

Application-problems

Equations and inequalities, pre-calculus, hinsdale south high school - darien-il.

Recommended for you

Students also viewed.

• 3-4 HW - homework
• 2-27 HW - homework
• 2-6 HW - homework
• 1-26 HW Part 2 - homework
• 1-10 HW - homework
• PCWL OTL 9A-8 Worksheet

Related documents

• 04-09 PC U05A 4.1 WS2 - Prametric Functions Modeling Planar Motion
• 04-18 PC U05A 4.7 WS7 - Parameterization of Implicitly Defined Functions
• WS 4.7 KEY - math worksheet
• Final Solutions to Pre Calc Final
• Reflection Refraction Diffractionand Interference Practice-1
• Unit Circle

Preview text

Ross program 2024 application problems.

This document is one part of the application to the Ross Mathematics Program, and will remain posted at rossprogram/students/to-apply from Jan- uary through March. The deadline for applications is March 15, 2024. The Admissions Committee will start reading applications on March 16. You are not expected to answer every question perfectly; rather, take this application as an opportunity to explore some beautiful mathematics! We are interested in seeing how you approach unfamiliar, open-ended math problems, and we encourage you to write up your discoveries and conjectures, even if you can’t prove them. We believe that the most valuable part of a problem is the time spent thinking on it, and your application should reflect this: we are not looking for quick answers written in minimal space. Instead, we hope to see evidence of your explorations, conjectures, proofs, and generalizations written in a readable format. If you make progress on these four problems (even if you don’t solve them completely), we encourage you to submit your Ross application. Submit your own work on these problems. If you’ve seen one of the problems before (e. in a class or online), please include a reference along with your solution. Admission factors include the quality of mathematical exposition and the questions you pose, as well as the completeness and correctness of your solutions to those questions.

A polynomial is integral when it has integer coefficients. The square root of 2 is a solution to the integral polynomial equation x 2 − 2 = 0. A number is rational when it can be expressed as ab for integers a and b (with b ̸= 0). A number is irrational when it is not rational.

(a) Suppose c is a non-square integer. (That is, c ̸= n 2 for any n.) Explain why

c is not rational. Similarly, if c is a non-cube integer, does it follow that 3

c is irrational?

(b) Find an integral polynomial equation that has α =

5 as a solution. Show that α is irrational.

(c) Let a and b be integers. Find an integral polynomial equation which has

b as a solution. Must

b be irrational? If a ̸= b, must

a − √b be irrational?

(d) Formulate some generalizations. As a starting point, is β =

7 irrational? What about numbers like γ = 3

6 and δ = 3

It’s hard to keep up with the fashionable trends of the day, and mathematical fashion is no exception. The fashion season of 2024 has the following unspoken fashion rules:

1 is fashionable.

If a and b are fashionable numbers, then so is a+ 1 b.

All other numbers are “so last year” and thus not fashionable.

(a) Find the smallest and largest fashionable numbers, and prove that they are the smallest and largest.

(b) Which numbers are fashionable? Can you characterize the set of all fashionable numbers?

(c) Word on the street is that in 2025, the fashion rules will be the same except for “ 1 is fashionable”. Explore how the set of fashionable numbers changes if we begin with a different starting set of numbers. For example, what if 2 and

3 are the given fashionable numbers?

We’d like for you to define the squarilarity of two-dimensional shapes. The squarilarity should be a number between 0 and 1 quantifying how much a shape looks like a square. All squares should have squarilarity equal to 1 , but aside from that restriction you can decide how to assign numbers to various shapes. We welcome and are interested in seeing any ideas you have. It may be a good idea to start thinking of squarilarity definitions for simple shapes, and then expanding to more complicated shapes. Ultimately, for whatever definition(s) you come up with, we’d like for you to do the following.

(a) Specify the class of shapes for which your definition applies.

(b) State your definition of squarilarity for the shapes you’re considering.

(c) Verify that the squarilarity is always between 0 and 1 , and verify that the squarilarity of any square is 1.

(d) Explore the implications of your definition! Compute the squarilarity of a few shapes, and make observations of patterns you notice. Is your definition of squarilarity a good one?

• Multiple Choice

Topic : Equations and Inequalities

Subject : pre-calculus.

• More from: Pre-Calculus Honors 703   Documents Go to course