t test hypothesis sample size

Z-test and T-test sample size calculator

T-test sample size calculator, and z-test sample size calculator, distribution, calculators.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.3: The Independent Samples t-Test Formula

• Last updated
• Save as PDF
• Page ID 50052

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Before we can use the formula, it is important to understand what it can tell us and how it gets there. The independent samples t- test formula looks quite complicated but is meant to tell us something that is conceptually fairly simple: The obtained t- value tells us far apart the two group means are using standard error. Another way to say this is that it tells us how many standard errors apart the two group means are. It does this by taking the difference in the sample means and dividing it by the standard error. The difference in means is calculated in the numerator of the formula and the pooled standard error is calculated in the denominator of the formula. The standard error (\(SE\)) used is known as a pooled standard error because it is calculated by putting information from both groups together (also known as pooling information ). Therefore, we can understand the formulas main construction and outcomes as follows:

\[t=\dfrac{\text { difference in sample means }}{\text { pooled standard error }}=\text { how many SEs apart the two sample means are } \nonumber \]

The numerator focuses on the difference between the mean of Group 1 and the mean of Group 2. This is the core of the formula because the hypotheses tested using an independent samples t -test are specifically asking whether these two means differ. Therefore, you can think of the numerator as the main focus of the formula and the denominator as taking into account other necessary information and adjustments. This will be true for the main format used for all three versions of the t- test in this book. The denominator of the independent samples t- test formula is used to take into account the error in the samples (via the pooled standard error).

The formula contains six symbols which represent and, thus, must be replaced with specific values. The independent samples t -test formula is as follows:

\[t=\dfrac{\bar{X}_1-\bar{X}_2}{\sqrt{\left[\dfrac{\left(n_1-1\right) s_1^2+\left(n_2-1\right) s_2^2}{n_1+n_2-2}\right]\left[\dfrac{n_1+n_2}{n_1 \times n_2}\right]}} \nonumber \]

The \(d f\) is the sum of \(n – 1\) for each group (or total \(n\) minus 2) and appears in the formula’s denominator.

The numerator asks for the mean of Group 1 and the mean of Group 2. These will be used to calculate the difference in means. The denominator asks for the sample size for Group 1, the sample size for Group 2, the variance for Group 1, and the variance for Group 2. These four things will be used to calculate the pooled standard error. Thus, the formula requires we know three basic things about each of the two groups so that we can plug them in and solve: mean, variance, and sample size.

Though the formula looks very complex, focusing on a few things can help us see that it is manageable. First, though there appear to be many symbols in the formula there are only six and the simplest one of them, sample size, appears the most often. Thus, the majority of the formula is just asking us to input sample sizes. Second, the mathematical operations required are ones most of us are familiar with. Operations refer to mathematical actions we take. The operations this formula requires include: adding, subtracting, multiplying, dividing, squaring (if converting SD to variance), and square rooting. Though the formula requires us to do many steps, each step only includes one of these six basic operations (and we can use calculators to make the more challenging steps of squaring and square rooting easier).

Notice that the formula includes all three components that impact statistical power (see Chapter 6 for a review of the components of power):

• The size of the change, difference, or pattern observed in the sample
• The sample size
• The size of the error in the sample statistic(s)

The first component, size of difference, is being incorporated in the numerator. The denominator is a bit more complex and it can be hard to see what it is doing so let’s take a moment to consider its role. The denominator allows necessary adjustments to be made that incorporate the other two components of statistical power: sample size and error. Error is being measured using the variance (which is the squared version of standard deviation) of each group. These components are both incorporated into the formula. The way sample sizes and variances are put together in the denominator is used to find the pooled standard error. Pooled standard error, therefore, takes into account two of the three components of power: the size of the sample and the size of the error.

Let’s take a moment to see the connection between standard error for one group (which we reviewed in Chapter 6) and standard error when it is pooled so that it takes into account two groups. Standard error for a single sample is found using this formula:

\[S E=\dfrac{\sigma}{\sqrt{n}} \nonumber \]

The independent samples t- test needs to pool this from two separate groups. It does so by first finding the pooled standard deviation (because there are two groups so there are two standard deviations) and adjusting that by a calculation of samples sizes. The left section of the denominator is calculating the pooled standard deviation. The pooled standard deviation (\(S_{\text {pooled }}\) or \(S_{p}\)) is the weighted average of the standard deviation of two or more groups. When we say an average is “weighted” it means that proportionally more “weight” is given to groups with larger sample sizes. Another way of saying this is that a weighted average takes into account any differences in sample size so that the group(s) with more cases (i.e. larger sample sizes) more heavily impact the value being calculated. This is how pooled standard deviation can be found when group variances are approximately even:

\[S_p=\sqrt{\left[\dfrac{\left(n_1-1\right) s_1^2+\left(n_2-1\right) s_2^2}{n_1+n_2-2}\right]} \nonumber \]

You may wonder why pooled standard deviation is calculated using variances and sample sizes rather than standard deviations and sample sizes. Recall from Chapter 4 that variance is used when we actually want the standard deviation but still have some work to do before we do the final step of square rooting. Notice that the \(S_p\) formula asks us to do calculations with variances and sample sizes but that those are all under a square root sign. Thus, we are using variance in route to finding the pooled standard deviation (which we will get to by square rooting as the last step of the \(S_p\) formula).

This needs to be further adjusted to go from pooled standard deviation to pooled standard error. Within the brackets on the right side of the denominator, we see the use of just the sample sizes. That piece is also under the square root sign so, on its own, it looks like this:

\[\sqrt{\left[\dfrac{n_1+n_2}{n_1 \times n_2}\right]} \nonumber \]

The presence of this piece changes the denominator of the formula from just finding the \(S_p\) into a formula for finding pooled standard error (\(S E_p\)). It is doing the same work that is done by the denominator of the \(SE\) formula for one group. Therefore, the formula for pooled standard error for an independent samples t -test looks like this:

\[S E_p=\left(\sqrt{\left[\dfrac{\left(n_1-1\right) s_1^2+\left(n_2-1\right) s_2^2}{n_1+n_2-2}\right]}\right)\left(\sqrt{\left[\dfrac{n_1+n_2}{n_1 \times n_2}\right]}\right) \nonumber \]

This can rewritten for (slightly more) simplicity (though, admittedly, it still looks a bit complex) as follows:

\[S E_p=\sqrt{\left[\dfrac{\left(n_1-1\right) s_1^2+\left(n_2-1\right) s_2^2}{n_1+n_2-2}\right]\left[\dfrac{n_1+n_2}{n_1 \times n_2}\right]} \nonumber \]

Therefore, the denominator of the independent samples t -test formula is the formula for pooled standard error for the test.

Let’s put the numerator and denominator together. The numerator is used to find the difference in the means. The denominator is used to find the relevant standard error for the formula. Finally, the formula tells us to divide the numerator by the denominator. When we do, we get a t- value which tells us how many standard errors the two means are apart.

Thus, we have come full circle and can now (hopefully) see why the formula can be thought of as follows:

\[t=how\; many\; standard\; errors\; apart\; the\; two\; sample\; means\; are \nonumber \]

Interpreting Obtained t-Values

Obtained t- values have two components: a magnitude and a direction. The magnitude is the absolute value of t and it represents how many standard errors the mean of one sample is from the mean of the other sample. The larger the value, the farther apart the two means are. As the t- value increases, the evidence for the research hypothesis and against the null hypothesis also increases. Conversely, as the t- value decreases, the evidence for the research hypothesis and against the null hypothesis also decreases. Thus, researchers are generally hoping for larger t values. The other component of t is its direction. When t is positive, it indicates that Group 1 had the higher mean than Group 2. Conversely, when t is negative, it indicates that Group 1 had the lower mean than Group 2. If the obtained t- value was 0.00, it would indicate that the means were zero standard errors apart (which is the same as saying the means were equal). If, for example, the obtained t- value was 3.00 it would indicate that the means of the two groups were three standard errors apart and that Group 1 had the higher mean. However, if the obtained t- value was -3.00 it would indicate that the two means were three standard errors apart and that Group 2 had the higher mean.

When testing a two-tailed (non-directional) hypothesis, only the magnitude needs to be considered to determine whether a result is significant. This is because a two-tailed hypothesis will be significantly supported if the difference in the means is sufficiently large regardless of which group mean was higher. However, when testing a one-tailed (directional) hypothesis, both magnitude and direction need to be considered. When it is hypothesized that Group 1 will have the higher mean than Group 2, the hypothesis will be significantly supported if the difference in the means is sufficiently large and the result is positive. When it is hypothesized that Group 2 will have the higher mean than Group 1, the hypothesis will be significantly supported if the difference in the means is sufficiently large and the result is negative. Thus, the direction of the results must match the direction of the hypothesis when using a one-tailed test of significance.

Alternative Ways to Write the Independent Samples t-Test Formula.

You may see the independent samples t- test written other ways. One common version is this:

\[t=\dfrac{\bar{X}_1-\bar{X}_2}{\sqrt{\left[\dfrac{S S_1+S S_2}{n_1+n_2-2}\right]\left[\dfrac{n_1+n_2}{n_1 \times n_2}\right]}} \nonumber \]

Another common version is this:

\[t=\dfrac{\bar{X}_1-\bar{X}_2}{\sqrt{\left[\dfrac{S S_1+S S_2}{n_1+n_2-2}\right]\left[\dfrac{1}{n_1}+\dfrac{1}{n_2}\right]}} \nonumber \]

These formulas are just different ways of getting to the same end result which some people find more or less intuitive. Let’s take a quick look at the variations in these formulas and how they are equivalent to what is in the version of the formula shown earlier. First, both of these versions use sum of squares (\(SS\)) in place of adjusted sample size multiplied by variance for each group. This is because variance is calculated by dividing \(SS\) by adjusted sample size (calculated as \(n – 1\) when working with samples). Thus, if we multiple variance by \(n – 1\) it turns it back into \(SS\).

Variance Formula: \(s^2=\dfrac{\Sigma(X-\bar{X})^2}{n-1}\)

Sum of Squares Formula: \(S S=\Sigma(X-\bar{X})^2\)

We can write it out to demonstrate. Variance times adjusted sample size is equal to SS because the adjusted sample sizes cancel out like so:

For this reason, \(SS\) can be used in place of \((n-1) s^2\) for each group in the denominator of the formula.

The other option for rewriting the formula is to use \(\left[\dfrac{1}{n_1}+\dfrac{1}{n_2}\right]\) in place of \(\left[\dfrac{n_1+n_2}{n_1 \times n_2}\right]\) in the right side of the denominator of the formula. These are just two way one can write the same things.

\[\left[\dfrac{1}{n_1}+\dfrac{1}{n_2}\right]=\left[\dfrac{n_1+n_2}{n_1 \times n_2}\right] \nonumber \]

Therefore, though we have seen three different ways to write the independent samples t -test formula, they are all simply different ways or writing the same mathematical concepts and steps and, thus, will all yield the same result.

Reading Review 8.2

• What is being calculated and represented by the numerator of the independent samples t test formula?
• What is being calculated and represented by the denominator of the independent samples t -test formula?
• Without making a determination of significance, how might t = 0.00 be interpreted?
• Without making a determination of significance, how might t = 1.46 be interpreted?
• Without making a determination of significance, how might t = -3.75 be interpreted?

Formula Components

Now that we have taken some time to understand the construction of the independent samples t- test formula, let’s focus on how to actually use it, starting with identifying all of its parts.

In order to solve for t , six things must first be known:

\(\bar{X}_1\) = the mean for Group 1

\(\bar{X}_2\) = the mean for Group 2

\(S_1^2\) = the variance for Group 1

\(S_2^2\) = the variance for Group 2

\(n_1\) = the sample size for Group 1

\(n_2\) = the sample size for Group 2

We use the raw scores from each group to calculate their respective means, variances, and sample sizes.

Formula Steps

The steps are shown in order and categorized into two sections: A) preparation and B) solving. I recommend using this categorization to help you organize, learn, and properly use all inferential formulas. Preparation steps refer to any calculations that need to be done before values can be plugged into the formula. For the independent samples t- test this includes finding the descriptive statistics that make up the six components of the formula for each group (listed in the section above). Once those are known, the steps in section B can be used to yield the obtained value for the formula. The symbol for the obtained value for each t -test is t . Follow these steps, in order, to find t.

Section A: Preparation

• Find \(n\) for Group 1.
• Find \(\bar{x}\) for Group 1.
• Find \(s^2\) for Group 1.
• Find \(n\) for Group 2.
• Find \(\bar{x}\) for Group 2.
• Find \(s^2\) for Group 2.

Section B: Solving

• Write the formula with the values found in section A plugged into their respective locations.
• Solve the numerator by subtracting the mean of Group 2 from the mean of Group 1.
• Multiply variance for Group 1 by \(n – 1\) for Group 1 to get the \(SS\) for Group 1.
• Multiply variance for Group 2 by \(n – 1\) for Group 2 to get the \(SS\) for Group 2.
• Add the \(SS\) for Group 1 (which is the result of step 3a) to the \(SS\) for Group 2 (which is the result of step 3b). This gives you total \(SS\).
• Find the degrees of freedom (\(d f\)) by adding the sample size for Group 1 to the sample size for Group 2 and then subtracting 2 from that total.
• Divide the total SS (which is result of step 3c) by the \(d f\) (which is the result of step 3d).
• Add the sample size of Group 1 to the sample size of Group 2 to get the total sample size.
• Multiply the sample size of Group 1 by the sample size of Group 2.
• Divide the total sample size (which is the result of step 4a) by the product of sample sizes (which is the result of step 4b).
• Multiply the left side of the denominator (which is the result of step 3e) by the right side of the denominator (which is the result of step 4c).
• Square root the denominator (which means square root the result of step 5) to get the pooled standard error for the formula.
• Finally, divide the numerator (which is the result of step 2) by the pooled standard error (which is the result of step 6) to get the obtained t -value.

• Number System and Arithmetic
• Probability
• Mensuration
• Trigonometry
• Mathematics

T-Test in Statistics: Formula, Types and Steps

T-Test is a method used in statistics to determine if there is a significant difference between the means of two groups and how they are related. In T-Test statistics, the sample data is a subset of the two groups that we use to draw conclusions about the groups as a whole. 

T-Test in Statistics

For example, if we want to know the average weight of mangoes grown on a farm, the population would consist of all the mangoes that grew on the farm. However, it would be time-consuming to weigh each mango. Instead, we could take a sample of mangoes from trees at different locations on the farm and use their weights to make inferences about the average weight of all the mangoes grown on the farm.

T-Test Definition

T-Test is a statistics method to determine significance changes between means of two groups. It helps us to determine whether the data sets belong to the same group or not. This comparison is often called a T-test.

T-Test Formula

There is no specific formula for T-Test, as it is divided into various types such as One Samples T-Test, Independent Samples T-test, etc. which are used as per the need. The formula used in each type is defined under the specific headings. The formula allows us to calculate a T-value which helps to make a comparison between the data sets.

Value of T-Test

The value obtained by substituting required values to the t-test formula is called the t-value. A larger T-value implies that the sets belong to a different population, while a smaller T-value implies that they belong to the same population. The formula is comprised of the values of mean, standard deviation and variance of the data sets under consideration.

How to Calculate T Value in T-Test

To calculate T-value in T-Test, we can use the following steps:

Step 1: To perform a T-test, two hypotheses namely the null hypothesis and the alternative hypothesis are defined which have different meanings for different types of T-tests.

Step 2: And, a value for the level of significance is defined which signifies the probability of making a Type I error, which implies the rejection of the null hypothesis while it is actually true. Commonly used values of level of significance are 0.05 (5%) and 0.01 (1%).

Step 3: A higher significance level, such as α = 0.05, provides a higher tolerance for Type I errors, meaning that it is more likely to reject the null hypothesis even when it is true.

Step 4: On the other hand, a lower significance level, such as α = 0.01, reduces the risk of Type I errors but it may increase the chances of accepting the null hypothesis when it is actually false, resulting in a Type II error.

Types of T-Test

Below are the three types of T-Test mentioned below.

• One Sample T-test
• Independent Samples T-test
• Paired Samples T-test

Let’s discuss these types in detail as follows:

One Sample T-Test

As the name implies, this test is used when we have one data set for a sample and we need to determine whether this data set belongs to a particular population or not. The mean value for the population data must be known in this case. The formula to determine T-value, in this case, is as follows:

t = (x̄ – μ) / (σ / √n) Where, t is the t-value, x̄ is the Sample mean, μ is the Population mean, σ is the Sample standard deviation, and n is the Sample size.

Steps to Calculate T Value One Sample T-Test 

To perform the One Sample T-test, the steps listed below are generally followed:

Step 1: State a null hypothesis and an alternative hypothesis. The null hypothesis assumes that the sample mean and the known population mean (μ) are equal, while the other assumes that the sample mean is different from the population mean.

Step 2: Define values for the level of significance (α) and the degree of freedom (df). The degree of freedom equals (n – 1) for this case.

Step 3: Calculate the t-value using the formula stated above by putting all the known values of the sample mean (x̄), sample standard deviation (σ), the population mean (μ), and the sample size (n).

Step 4: Determine the associated p-value with the t-value using a t-distribution table.

Step 5: Compare the p-value to the level of significance. If the p-value is less than the level of significance, reject the null hypothesis and conclude that the sample mean is significantly different from the population mean. Otherwise, conclude that there is no significant difference between the sample mean and the population mean.

Independent Samples T-Test

As the name suggests, an Independent samples T-test is used when we need to compare the statistical means of two independent samples or groups. It helps us determine whether there is a significant difference between the means of the two groups. If there is a significant difference, it suggests that the groups likely have different population means; otherwise, they have the same population means.

For example, when an investigation aims to determine if there is a significant difference in the mean scores between athletes who follow a specific training camp (Team A) and those who do not (Team B), an independent samples t-test can be conducted.

This test is performed using either of two assumptions made about variances of the samples, one assumes equal variances for the sample and the other assumes unequal variances for the samples.

Unequal Variances T-Test

Under this test, variances of two groups considered are assumed to be equal. This is appropriate when we are uncertain about the variances of the two groups considered. The formula to calculate T-value, in this case, is as follows:

t = (x̄ 1 – x̄ 2 ) / √((σ 1 2 /n 1 ) + (σ 2 2 /n 2 )) Where, x̄ 1 is the sample mean of Group 1, x̄ 2 is the sample mean of Group 2, σ 1 is the sample standard deviation of Group 1, σ 2 is the sample standard deviation of Group 2, n 1 is the sample size of Group 1, and n 2 sample size of Group 2.

Equal Variance T-Test

Under this test, variances of two groups considered are assumed to be equal. This is appropriate when we have some assurance about variances of data considered to be equal. The formula to calculate T-value, in this case, is similar to the above formula with a slight change that σ 1 = σ 2 = σ.

t = (x̄ 1 – x̄ 2 ) / √(σ 2 (1/n 1 + 1/n 2 )) Where, x̄ 1 is the sample mean of Group 1, x̄ 2 is the sample mean of Group 2, σ is the standard deviation of both groups, n 1 is the sample size of Group 1, and n 2 sample size of Group 2.

T Test for Independent Samples

The steps listed below are generally followed to perform this test:

Step 1: State a null hypothesis and an alternate hypothesis. The null hypothesis assumes that the means of the two groups are equal (x̄ 1 = x̄ 2 ), while the other assumes that the means of the two groups are significantly different (x̄ 1 ≠ x̄ 2 ).

Step 2: Define the values for the level of significance (α) and the degrees of freedom (df). The degree of freedom equals (n 1 + n 2 – 2) in this case.

Step 3: Calculate the t-value from the formula defined above after obtaining the required data related to each group.

Step 4: Find the critical t-value from a t-distribution table with the corresponding degrees of freedom and level of significance.

Step 5: If the calculated t-value is greater than the critical t-value, then reject the null hypothesis. This indicates that there is a significant difference between the means of the two groups. Otherwise, the null hypothesis is not rejected. And, this suggests that there is no significant difference between the means of the two groups.

Paired Samples T-Test

The Paired samples t-test is used when we want to compare the means of two related groups or samples. For example, we may use this test to compare the average scores of the players of an athletics team before and after a training program. To calculate the t-value in this case, the following formula is used,

t = (x̄ d – μ d ) / (σ d / √n) Where: t is the t-value, x̄ d is the sample mean of the differences between the paired observations, μ d isthe population mean difference, σ d is the sample standard deviation of the differences, n is the number of paired observations.

Steps for Paired Samples T-Test

Following are the steps to perform this type of T-test:

Step 1: State the null hypothesis which assumes that there is no significant difference between the statistical means of the paired observations (μ d = 0) while the alternative hypothesis assumes that there is a significant difference between the statistical means of the paired observations (μ d ≠ 0).

Step 2: Match each observation in one group with a corresponding observation in the other group.

Step 3: Calculate the differences between each paired observation and then, calculate the mean of the differences (x̄ d ), and the sample standard deviation of the differences (σ d ). Furthermore, calculate the t-value from the formula.

Step 4: Obtain the critical t-value from a t-distribution table corresponding to the chosen level of significance (α) and degree of freedom (df). The degree of freedom (df) equals (n – 1) in this case.

Step 5: If the calculated t-value is greater than the critical t-value, then reject the null hypothesis. This indicates a significant difference in the sample before and after the intervention. Otherwise, it can be concluded that there is no significant difference in the sample before and after the intervention.

T-Distribution Table

A T-Distribution table is used to obtain a critical t-value that is used as a reference to the calculated t-value for obtaining further results. Critical t-value depends on values of the level of significance and degrees of freedom. A concise form of the table for critical t-values is as follows for your reference:

Solved Problems of T-Test Formula

Problem 1: Determine whether the average weight of a sample of 20 mangoes is significantly different from the population’s average weight of 70 grams. The sample mean weight is 70.55 grams, and the sample standard deviation is 2.82 grams. Use one sample T-test.

To perform a T-test, first of all, we define two hypotheses: Null hypothesis: The sample mean weight of mangoes is equal to the known population mean. (i.e., 70 grams). Alternative hypothesis: The sample mean weight of mangoes is not equal to the known mean value. Then, determine the degrees of freedom (d f ): d f = n – 1 = 20 – 1 = 19 and define the level of significance(α) as 0.05 for this case. Next, determine the t-value from the formula, t = (70.55 – 70) / (2.82 / √20) ⇒ t ≈ 1.041 From the t-distribution table, we find 1.041 < 2.093. (i.e. p-value for α = 0.05). So, the null hypothesis is true. Thus, we conclude that the sample does not vary significantly from the population.

Problem 2: Determine if there is a significant difference in the average scores between the two teams. The following data is given:  Team A: Score: 65, 68, 70, 63, 67 Team B: Score: 62, 66, 69, 64, 68

According to the question, we come to know that we need to perform an Independent Samples T-test. Set up the null hypothesis and alternative hypothesis: Null hypothesis: The means of the two groups are equal (μ A = μ B ). Alternative hypothesis: The means of the two groups are not equal (μ A ≠ μ B ). Next, we calculate the sample means (x̄ A and x̄ B ) and sample standard deviations (σ A and σ B ): Team A: Sample size (n A ) = 5 Sample mean (x̄ A ) = (65 + 68 + 70 + 63 + 67) / 5 = 66.6 Sample standard deviation (σ A ) ≈ 2.607 Team B: Sample size (n B ) = 5 Sample mean (x̄ B ) = (62 + 66 + 69 + 64 + 68) / 5 = 65.8 Sample standard deviation (σ B ) ≈ 2.588 Now, we calculate the t-value using the formula: t = (x̄ A – x̄ B ) / √((σ A 2 / n A ) + (σ B 2 / n B )) ⇒ t = (66.6 – 65.8) / √{(2.607 2 /5) + (2.588 2 /5)} ⇒ t ≈ 0.296 Then, determine the degrees of freedom (df):  df = n A + n B – 2 = 5 + 5 – 2 = 8  and set the level of significance as 0.05.  From the table, we get the critical t-value as 2.306. As the calculated t-value is less than the critical t-value, we conclude that the null hypothesis is not rejected, which suggests that there is no significant difference between the average scores of the two teams.

Problem 3: You need to assess the effectiveness of a new teaching scheme by comparing the test scores of the same group of students before and after the implementation of the scheme. The following data is given: Before scores: 76, 88, 65, 56, 76 After scores: 85, 95, 75, 60, 81 Determine if there is a significant difference in the average test scores before and after the implementation of the scheme.

Here, we need to perform a Paired Samples T-test, as we need to compare data of the same sample. Set up the null hypothesis and alternative hypothesis: Null hypothesis: The population mean difference between the before and after scores are zero (μ d = 0). Alternative hypothesis: The population mean difference between the before and after scores is not zero (μ d ≠ 0). Next, calculate the differences between the paired observations: Difference (d) = After score – Before score d 1 = 85 – 76 = 9 d 2 = 95 – 88 = 7 d 3 = 75 – 65 = 10 d 4 = 60 – 56 = 4 d 5 = 81 – 76 = 5 Now, calculate the sample mean (x̄d) and sample standard deviation (σ d ) of the differences: Sample size (n) = 5 Sample mean (x̄ d ) = (d 1 + d 2 + d 3 + d 4 + d 5 ) / 5 = (9 + 7 + 10 + 4 + 5) / 5 = 7 Sample standard deviation (σ d ) ≈ 2.828 Then, calculate the t-value using the formula: t = (x̄ d – μ d ) / (σ d / √n)  ⇒ t = (7 – 0) / (2.828 / √5) ⇒ t ≈ 5.535 Next, calculate the value of degrees of freedom (df):  df = n – 1 = 5 – 1 = 4.  And, define the level of significance(α) as 0.05.  Now, from the t-distribution table, we find that the critical t-value is 2.776. As the calculated t-value is greater than the critical t-value ( 5.535 > 2.776), thus, the null hypothesis is rejected. And we conclude that there is a significant difference in the average test scores before and after the implementation of the scheme.

T-Test in Statistics – FAQs

What is a t-test in statistics.

T-Test is the test in statistics to derive some conclusions for a population which is based upon some sample data using values of means and variances. 

When is a T-Test used?

The test is basically used to determine whether there is any significant difference in the statistical means of two samples of the data considered. The purpose to determine this can be to check if a sample data set belongs to the population data set, or if there is an effect of any variation on the data values before or after any specific treatment/intervention.

What are the Different Types of T-Tests?

There are three types of T-tests that are used as per the situation, listed as follows: One-sample T-test: It is used when we need to compare the mean of a single sample to a known (or assumed) population mean value. Independent T-test: It is used when we need to compare the means of two independent groups. Paired T-test: It is used to compare the means of two related or paired groups.

What does the T-Value obtain from the T-Test Formula Indicate?

The t-value indicates the magnitude of the difference between the means relative to the variability within the groups. A larger t-value suggests a greater difference between the means.

Are there any Assumptions related to Sample Data in Performing a T-Test on it?

The t-test assumes that the data within each group are normally distributed, the variances of the two groups are equal (in the case of an independent t-test), the observations are independent, and the data points represent their respective populations.

What are the Limitations of the T-Test?

The t-test assumes that the data meet the assumptions of normality, independence, and equal variances (in the case of an independent t-test). If these assumptions are not true, it can lead to inaccurate or misleading results. Also, the test is sensitive to outliers, and may not give accurate results for small sample sizes.

Similar Reads

• T-Test in Statistics: Formula, Types and Steps T-Test is a method used in statistics to determine if there is a significant difference between the means of two groups and how they are related. In T-Test statistics, the sample data is a subset of the two groups that we use to draw conclusions about the groups as a whole.  For example, if we want 14 min read
• Data Types in Statistics Data is a simple record or collection of different numbers, characters, images, and others that are processed to form Information. In statistics, we have different types of data that are used to represent various information. In statistics, we analyze the data to obtain any meaningful information an 6 min read
• How to Find p Value from Test Statistic P-values are widely used in statistics and are important for many hypothesis tests. But how do you find a p-value? The method can vary depending on the specific test, but there's a general process you can follow. In this article, you'll learn how to find the p-value, get an overview of the general s 9 min read
• What are the types of statistics? Answer: There are majorly 2 different types of statistics i.e. Descriptive and Inferential Statistics.Statistics is a branch of science that deals with the ability to grasp different outcomes from it and foresee several possibilities of various events. It is used to capture the various possible indi 3 min read
• Introduction of Statistics and its Types Statistics and its Types: Statistics is a branch of math focused on collecting, organizing, and understanding numerical data. It involves analyzing and interpreting data to solve real-life problems, using various quantitative models. Some view statistics as a separate scientific discipline rather th 15+ min read
• How to Calculate Test Statistic In statistical hypothesis testing, a test statistic is a crucial tool used to determine the validity of the hypothesis about a population parameter. This article delves into the calculation of test statistics exploring its importance in hypothesis testing and its application in real-world scenarios. 8 min read
• What are some of the important formulae used in statistics? Statistics is a branch of science that is used for data collection, evaluation, and summarising. It summarises the data in a mathematical format. Statistics is used mainly to gain an understanding of the data and focus on various applications. It is used to collect facts and figures about the data s 7 min read
• Type I and Type II Errors Type I and Type II Errors are central for hypothesis testing in general, which subsequently impacts various aspects of science including but not limited to statistical analysis. False discovery refers to a Type I error where a true Null Hypothesis is incorrectly rejected. On the other end of the spe 10 min read
• How to find the sample size for t test in R? When designing a study, determining the appropriate sample size is crucial to ensure sufficient power to detect a significant effect. For a t-test, sample size calculation involves understanding various parameters such as effect size, significance level, power, and the type of t-test used (one-sampl 4 min read
• Statistics Formulas Statistics is a branch of mathematics that deals with numerical data analysis. It presents the data in an organized manner. Statistics is a study of a collection of data, analysis it, interpretation, and presentation of data in a well-organized form. It allows us to interpret various results from th 5 min read
• How to Calculate the P-Value of an F-Statistic in R F-test is a statistical test and it produces the F-statistic which possesses F distribution under the null hypothesis. This article focuses on how we can compute the P-value of an F-statistic in R Programming Language. Finding P-value of an F statistic in R R provides us pf() function using which we 3 min read
• Statistics For Data Science Statistics is like a toolkit we use to understand and make sense of information. It helps us collect, organize, analyze, and interpret data to find patterns, trends, and relationships in the world around us. In this Statistics cheat sheet, you will find simplified complex statistical concepts, with 15+ min read
• Types of Statistical Data Analysis Statistics data analysis is a class of analysis that includes different techniques and methods for collection, data analysis, interpretation and presentation of data. Knowing the approach to data analysis is one of the crucial aspects that allows drawing a meaningful conclusion. In this article, the 7 min read
• What is x Bar in Statistics x̄ which is read as x bar is a fundamental concept for understanding and interpreting data in Statistics. x̄ also called as sample mean is a measure of central tendency i.e. the average value of given sample data points with a single value. In this article, we are going to learn what is x̄, how we c 10 min read
• Types of Statistical Series In statistics, data is often organized in series to facilitate analysis and interpretation. A statistical series refers to a set of observations arranged in a particular order based on one or more criteria. Understanding the different types of statistical series is crucial for effectively analyzing 13 min read
• A/B Testing vs Multivariate Testing A/B testing and multivariate testing are essential techniques in digital marketing and user experience optimization. Both methods help businesses improve website performance and user engagement, but they serve different purposes. A/B Testing involves comparing two versions of a single element to see 6 min read
• How to find the Standard deviation in Statistics? Answer: Standard deviation in statistics is calculated using formula:[Tex]s=\frac{\sqrt{\sum({x_i-\bar{x}})^2}}{N}[/Tex]Statistics is the study of data gathering, organization, interpretation, analysis, and presentation in mathematics. The primary goal of statistics is to plan the obtained data in t 3 min read
• Upper Tail Test of Population Proportion in R A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. The conventional steps that are followed while formulating the hypothesis test, are listed as follows State null hypothesis (Ho) and alternate hypo 2 min read
• Differences Between two-sample, t-test and paired t-test Statistical tests are essential tools in data analysis, helping researchers make inferences about populations based on sample data. Two common tests used to compare the means of different groups are the two-sample t-test and the paired t-test. Both tests are based on the t-distribution, but they hav 7 min read
• School Learning
• Maths-Class-12

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

t-test Calculator

Table of contents

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

When to use a t-test?

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

• A one-sample t-test;
• A two-sample t-test; and
• A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

• The data points are independent; AND
• The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Which t-test?

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Two-sample t-test

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

Paired t-test

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

How to do a t-test?

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

p-value from t-test

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

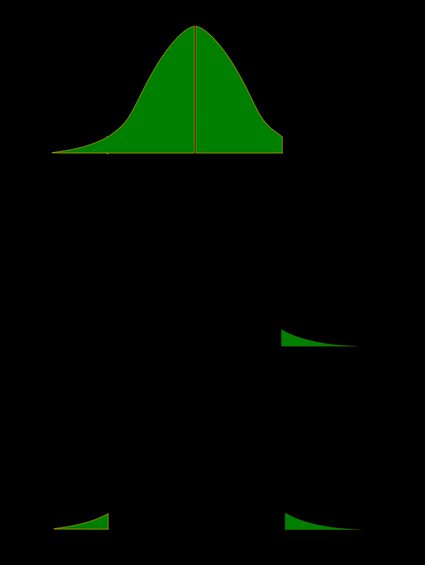
The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

t-test critical values

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

How to use our t-test calculator

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

One-sample t-test

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 ​ .

The alternative hypothesis is that the population mean is:

• different from μ 0 \mu_0 μ 0 ​ ;
• smaller than μ 0 \mu_0 μ 0 ​ ; or
• greater than μ 0 \mu_0 μ 0 ​ .

One-sample t-test formula :

• μ 0 \mu_0 μ 0 ​ — Mean postulated in the null hypothesis;
• n n n — Sample size;
• x ˉ \bar{x} x ˉ — Sample mean; and
• s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 ​ , and μ 2 \mu_2 μ 2 ​ , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 ​ − μ 2 ​ is:

• Different from Δ \Delta Δ ;
• Smaller than Δ \Delta Δ ; or
• Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

• μ 1 \mu_1 μ 1 ​ and μ 2 \mu_2 μ 2 ​ are different from one another;
• μ 1 \mu_1 μ 1 ​ is smaller than μ 2 \mu_2 μ 2 ​ ; and
• μ 1 \mu_1 μ 1 ​ is greater than μ 2 \mu_2 μ 2 ​ .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p ​ is the so-called pooled standard deviation , which we compute as:

• Δ \Delta Δ — Mean difference postulated in the null hypothesis;
• n 1 n_1 n 1 ​ — First sample size;
• x ˉ 1 \bar{x}_1 x ˉ 1 ​ — Mean for the first sample;
• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• n 2 n_2 n 2 ​ — Second sample size;
• x ˉ 2 \bar{x}_2 x ˉ 2 ​ — Mean for the second sample; and
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 ​ + n 2 ​ − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

• The pre- and post-means are different from one another (treatment has some effect);
• The pre-mean is smaller than the post-mean (treatment increases the result); or
• The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 ​ , ... , x n ​ be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 ​ , ... , y n ​ the respective post observations. That is, x i , y i x_i, y_i x i ​ , y i ​ are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i ​ := x i ​ − y i ​ . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 ​ , ... , d n ​ . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s  — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

t-test vs Z-test

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

• One-sample t-test;
• Two-sample t-test; and
• Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

• Subtract the null hypothesis mean from the sample mean value.
• Divide the difference by the standard deviation of the sample.
• Multiply the resultant with the square root of the sample size.

.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-1h42f0z{margin:auto;overflow:auto;overflow-wrap:break-word;word-break:break-word;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-1h42f0z .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-1h42f0z .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-1h42f0z .katex .katex-version::after{content:'0.13.13';}.css-1h42f0z .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-1h42f0z .katex .katex-html>.newline{display:block;}.css-1h42f0z .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-1h42f0z .katex .strut{display:inline-block;}.css-1h42f0z .katex .textbf{font-weight:bold;}.css-1h42f0z .katex .textit{font-style:italic;}.css-1h42f0z .katex .textrm{font-family:KaTeX_Main;}.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .texttt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-1h42f0z .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-1h42f0z .katex .mathrm{font-style:normal;}.css-1h42f0z .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-1h42f0z .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-1h42f0z .katex .amsrm{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathbb,.css-1h42f0z .katex .textbb{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-1h42f0z .katex .mathfrak,.css-1h42f0z .katex .textfrak{font-family:KaTeX_Fraktur;}.css-1h42f0z .katex .mathtt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathscr,.css-1h42f0z .katex .textscr{font-family:KaTeX_Script;}.css-1h42f0z .katex .mathsf,.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .mathboldsf,.css-1h42f0z .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-1h42f0z .katex .mathitsf,.css-1h42f0z .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-1h42f0z .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-1h42f0z .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-1h42f0z .katex .vlist-r{display:table-row;}.css-1h42f0z .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-1h42f0z .katex .vlist>span{display:block;height:0;position:relative;}.css-1h42f0z .katex .vlist>span>span{display:inline-block;}.css-1h42f0z .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-1h42f0z .katex .vlist-t2{margin-right:-2px;}.css-1h42f0z .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-1h42f0z .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-1h42f0z .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-1h42f0z .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-1h42f0z .katex .msupsub{text-align:left;}.css-1h42f0z .katex .mfrac>span>span{text-align:center;}.css-1h42f0z .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .mfrac .frac-line,.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline,.css-1h42f0z .katex .hdashline,.css-1h42f0z .katex .rule{min-height:1px;}.css-1h42f0z .katex .mspace{display:inline-block;}.css-1h42f0z .katex .llap,.css-1h42f0z .katex .rlap,.css-1h42f0z .katex .clap{width:0;position:relative;}.css-1h42f0z .katex .llap>.inner,.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{position:absolute;}.css-1h42f0z .katex .llap>.fix,.css-1h42f0z .katex .rlap>.fix,.css-1h42f0z .katex .clap>.fix{display:inline-block;}.css-1h42f0z .katex .llap>.inner{right:0;}.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{left:0;}.css-1h42f0z .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-1h42f0z .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-1h42f0z .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-1h42f0z .katex .sizing.reset-size1.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size1.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size1.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-1h42f0z .katex .sizing.reset-size1.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size1.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size1.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size1.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size1.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size1.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-1h42f0z .katex .sizing.reset-size1.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-1h42f0z .katex .sizing.reset-size1.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-1h42f0z .katex .sizing.reset-size2.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size2.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size2.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-1h42f0z .katex .sizing.reset-size2.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size2.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size2.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-1h42f0z .katex .sizing.reset-size2.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size2.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size2.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size2.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-1h42f0z .katex .sizing.reset-size2.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-1h42f0z .katex .sizing.reset-size3.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-1h42f0z .katex .sizing.reset-size3.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size3.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-1h42f0z .katex .sizing.reset-size3.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-1h42f0z .katex .sizing.reset-size3.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-1h42f0z .katex .sizing.reset-size3.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-1h42f0z .katex .sizing.reset-size3.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-1h42f0z .katex .sizing.reset-size3.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-1h42f0z .katex .sizing.reset-size3.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-1h42f0z .katex .sizing.reset-size4.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size4.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size4.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-1h42f0z .katex .sizing.reset-size4.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size4.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-1h42f0z .katex .sizing.reset-size4.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-1h42f0z .katex .sizing.reset-size4.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size4.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size4.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-1h42f0z .katex .sizing.reset-size4.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-1h42f0z .katex .sizing.reset-size4.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-1h42f0z .katex .sizing.reset-size5.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size5.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size5.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-1h42f0z .katex .sizing.reset-size5.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-1h42f0z .katex .sizing.reset-size5.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size5.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-1h42f0z .katex .sizing.reset-size5.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size5.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size5.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-1h42f0z .katex .sizing.reset-size5.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-1h42f0z .katex .sizing.reset-size5.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-1h42f0z .katex .sizing.reset-size6.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size6.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-1h42f0z .katex .sizing.reset-size6.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-1h42f0z .katex .sizing.reset-size6.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-1h42f0z .katex .sizing.reset-size6.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-1h42f0z .katex .sizing.reset-size6.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size6.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size6.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size6.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-1h42f0z .katex .sizing.reset-size6.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-1h42f0z .katex .sizing.reset-size6.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-1h42f0z .katex .sizing.reset-size7.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size7.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size7.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-1h42f0z .katex .sizing.reset-size7.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size7.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size7.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size7.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size7.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size7.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size7.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-1h42f0z .katex .sizing.reset-size7.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-1h42f0z .katex .sizing.reset-size8.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size8.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size8.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-1h42f0z .katex .sizing.reset-size8.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size8.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size8.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size8.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size8.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size8.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size8.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-1h42f0z .katex .sizing.reset-size8.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-1h42f0z .katex .sizing.reset-size9.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-1h42f0z .katex .sizing.reset-size9.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size9.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-1h42f0z .katex .sizing.reset-size9.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-1h42f0z .katex .sizing.reset-size9.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-1h42f0z .katex .sizing.reset-size9.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-1h42f0z .katex .sizing.reset-size9.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size9.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size9.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size9.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-1h42f0z .katex .sizing.reset-size9.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-1h42f0z .katex .sizing.reset-size10.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-1h42f0z .katex .sizing.reset-size10.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-1h42f0z .katex .sizing.reset-size10.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-1h42f0z .katex .sizing.reset-size10.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-1h42f0z .katex .sizing.reset-size10.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-1h42f0z .katex .sizing.reset-size10.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-1h42f0z .katex .sizing.reset-size10.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-1h42f0z .katex .sizing.reset-size10.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-1h42f0z .katex .sizing.reset-size10.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-1h42f0z .katex .sizing.reset-size10.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size10.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-1h42f0z .katex .sizing.reset-size11.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-1h42f0z .katex .sizing.reset-size11.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-1h42f0z .katex .sizing.reset-size11.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-1h42f0z .katex .sizing.reset-size11.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-1h42f0z .katex .sizing.reset-size11.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-1h42f0z .katex .sizing.reset-size11.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-1h42f0z .katex .sizing.reset-size11.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-1h42f0z .katex .sizing.reset-size11.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-1h42f0z .katex .sizing.reset-size11.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-1h42f0z .katex .sizing.reset-size11.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-1h42f0z .katex .sizing.reset-size11.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-1h42f0z .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-1h42f0z .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-1h42f0z .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-1h42f0z .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-1h42f0z .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-1h42f0z .katex .delimcenter{position:relative;}.css-1h42f0z .katex .op-symbol{position:relative;}.css-1h42f0z .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-1h42f0z .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-1h42f0z .katex .op-limits>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent .accent-body{position:relative;}.css-1h42f0z .katex .accent .accent-body:not(.accent-full){width:0;}.css-1h42f0z .katex .overlay{display:block;}.css-1h42f0z .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-1h42f0z .katex .mtable .arraycolsep{display:inline-block;}.css-1h42f0z .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-1h42f0z .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-1h42f0z .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-1h42f0z .katex .svg-align{text-align:left;}.css-1h42f0z .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-1h42f0z .katex svg path{stroke:none;}.css-1h42f0z .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-1h42f0z .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-1h42f0z .katex .stretchy::before,.css-1h42f0z .katex .stretchy::after{content:'';}.css-1h42f0z .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-1h42f0z .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-1h42f0z .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .x-arrow-pad{padding:0 0.5em;}.css-1h42f0z .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-1h42f0z .katex .x-arrow,.css-1h42f0z .katex .mover,.css-1h42f0z .katex .munder{text-align:center;}.css-1h42f0z .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-1h42f0z .katex .fbox,.css-1h42f0z .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-1h42f0z .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-1h42f0z .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-1h42f0z .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-1h42f0z .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-1h42f0z .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-1h42f0z .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-1h42f0z .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-1h42f0z .katex .mtr-glue{width:50%;}.css-1h42f0z .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-1h42f0z .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-1h42f0z .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-1h42f0z .katex-display{display:block;margin:1em 0;text-align:center;}.css-1h42f0z .katex-display>.katex{display:block;white-space:nowrap;}.css-1h42f0z .katex-display>.katex>.katex-html{display:block;position:relative;}.css-1h42f0z .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-1h42f0z .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-1h42f0z .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-1h42f0z body{counter-reset:katexEqnNo mmlEqnNo;}.css-1h42f0z .link-like{color:#007bff;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-1h42f0z code,.css-1h42f0z kbd,.css-1h42f0z pre,.css-1h42f0z samp{font-family:monospace;}.css-1h42f0z code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-1h42f0z figcaption,.css-1h42f0z caption{text-align:center;}.css-1h42f0z figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-1h42f0z h3{font-size:1.75rem;}.css-1h42f0z h4{font-size:1.5rem;}.css-1h42f0z .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-1h42f0z .mathBlock .katex{font-size:24px;text-align:left;}.css-1h42f0z .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-1h42f0z .videoBlock,.css-1h42f0z .imageBlock{margin-bottom:16px;}.css-1h42f0z .imageBlock__image-align--left,.css-1h42f0z .videoBlock__video-align--left{float:left;}.css-1h42f0z .imageBlock__image-align--right,.css-1h42f0z .videoBlock__video-align--right{float:right;}.css-1h42f0z .imageBlock__image-align--center,.css-1h42f0z .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-1h42f0z .imageBlock__image-align--none,.css-1h42f0z .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-1h42f0z .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-1h42f0z .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-1h42f0z .videoBlock__caption{text-align:left;}.css-1h42f0z table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-1h42f0z .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-1h42f0z .tableBlock thead,.css-1h42f0z .tableBlock thead th{border-bottom:1px solid #333!important;}.css-1h42f0z .tableBlock th,.css-1h42f0z .tableBlock td{padding:10px;text-align:left;}.css-1h42f0z .tableBlock th{font-weight:bold!important;}.css-1h42f0z .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-1h42f0z .tableBlock caption>p{margin:0;}.css-1h42f0z .tableBlock th>p,.css-1h42f0z .tableBlock td>p{margin:0;}.css-1h42f0z .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-1h42f0z .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-1h42f0z .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-1h42f0z .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-1h42f0z .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-1h42f0z .tableBlock [data-text-align='center']{text-align:center;}.css-1h42f0z .tableBlock [data-text-align='left']{text-align:left;}.css-1h42f0z .tableBlock [data-text-align='right']{text-align:right;}.css-1h42f0z .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-1h42f0z .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-1h42f0z .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-1h42f0z .tableBlock__font-size--xxsmall{font-size:10px;}.css-1h42f0z .tableBlock__font-size--xsmall{font-size:12px;}.css-1h42f0z .tableBlock__font-size--small{font-size:14px;}.css-1h42f0z .tableBlock__font-size--large{font-size:18px;}.css-1h42f0z .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-1h42f0z .tableBlock__border--bordered td,.css-1h42f0z .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-1h42f0z .tableBlock__border--borderless tbody+tbody,.css-1h42f0z .tableBlock__border--borderless td,.css-1h42f0z .tableBlock__border--borderless th,.css-1h42f0z .tableBlock__border--borderless tr,.css-1h42f0z .tableBlock__border--borderless thead,.css-1h42f0z .tableBlock__border--borderless thead th{border:0!important;}.css-1h42f0z .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-1h42f0z .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-1h42f0z .tableBlock__table-compactl th,.css-1h42f0z .tableBlock__table-compact td{padding:3px!important;}.css-1h42f0z .tableBlock__full-size{width:100%;}.css-1h42f0z .textBlock{margin-bottom:16px;}.css-1h42f0z .textBlock__text-formatting--finePrint{font-size:12px;}.css-1h42f0z .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-1h42f0z .textBlock__text-infoBox p{margin:0;}.css-1h42f0z .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-1h42f0z .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-1h42f0z .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-1h42f0z .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-1h42f0z .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-1h42f0z .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-1h42f0z .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-1h42f0z.css-1h42f0z{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-1h42f0z.css-1h42f0z:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-1h42f0z .js-external-link-button.link-like,.css-1h42f0z .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .js-external-link-button.link-like:hover,.css-1h42f0z .js-external-link-anchor:hover,.css-1h42f0z .js-external-link-button.link-like:active,.css-1h42f0z .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-1h42f0z .js-external-link-button.link-like:focus-visible,.css-1h42f0z .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-1h42f0z p,.css-1h42f0z div{margin:0;display:block;}.css-1h42f0z pre{margin:0;display:block;}.css-1h42f0z pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-1h42f0z pre:not(:first-child){padding-top:8px;}.css-1h42f0z ul,.css-1h42f0z ol{display:block margin:0;padding-left:20px;}.css-1h42f0z ul li,.css-1h42f0z ol li{padding-top:8px;}.css-1h42f0z ul ul,.css-1h42f0z ol ul,.css-1h42f0z ul ol,.css-1h42f0z ol ol{padding-top:0;}.css-1h42f0z ul:not(:first-child),.css-1h42f0z ol:not(:first-child){padding-top:4px;} Test setup

Choose test type

t-test for the population mean, μ, based on one independent sample . Null hypothesis H 0 : μ = μ 0  

Alternative hypothesis H 1

Test details

Significance level α

The probability that we reject a true H 0 (type I error).

Degrees of freedom

Calculated as sample size minus one.

Test results

LEARN STATISTICS EASILY

Learn Data Analysis Now!

Sample Size for t-Test: How to Calculate?

Are you aware that calculating the sample size for a t-test is a critical step in data analysis , which saves you time and money? Did you know that an adequate sample size makes your results more reliable? Despite its importance, many researchers collect and analyze their data without addressing this step, potentially compromising the reliability of their results. Fortunately, this often-overlooked step is quite simple!

In this article, we’ll present the correct way to calculate the sample size for a t-test using an excellent free statistical program.

The Problem

Calculating the sample size is necessary to determine how many participants are required to detect a significant effect. It may not be possible to detect an existing effect if the sample size is too small. However, large samples can waste time, resources, and money. Therefore, optimizing sample size is crucial.

Additionally, sample size calculation at the study design stage is increasingly required, for example, when seeking ethics committee approval for research projects involving humans or animals and subsequent publication.

The Solution

To calculate the sample size for the t-test, we will use G*Power, an excellent free program to calculate sample sizes for various analyses.

First,   download , install, and open the program.

Next, select the desired test, the independent samples t-test. Click on the  Tests: Means: Two independent groups  tab. Now, let’s fill in the fields!

Now, let’s fill in the fields!

1. Tail(s):  Choose ‘One’ if the test is one-tailed or ‘Two’ if the test is two-tailed. Use a one-tailed test if your alternative hypothesis is that the mean of one group is greater than the other. But, if your alternative hypothesis is that the means are different between the groups, without distinguishing which is higher or lower, use the two-tailed test. Base this hypothesis on existing knowledge in the study area. If unsure, leave the option at ‘Two.’

2. α err prob = significance level (α): Probability of rejecting the null hypothesis (H0) when it is true (type I error). Commonly used values are 0.05 or 0.01. A significance level of 0.05, for example, indicates a 5% risk of concluding that a difference exists when there is no actual difference.

3. Power (1 – β err prob) = Power of the Test (1 – β):  Probability of rejecting the null hypothesis if it is false, i.e., how well the test controls for type II error. Acceptable values are typically between 0.80 and 0.99. The higher the test’s power, the

4. Allocation ratio N2/N1 = Allocation ratio between groups N2/N1:  If you intend that the sample size of both groups is the same, then enter the value 1. Enter the required value if you want another allocation ratio between the groups.

❓ CONFUSED BY DATA ANALYSIS?

Our comprehensive guide will make it crystal clear, click to learn more.

5. Effect size d = Cohen’s effect size (d): This measure represents the strength of the difference detected between the tested groups. Conventionally, d = 0.20 is considered weak, d = 0.50 medium, and d = 0.80 strong. To set d for your sample size calculation, click “Determine =>,” and a new tab will open. In this new tab, we must input values for the two groups’ mean (Mean) and standard deviation (SD σ)

Suppose you’re at the stage of calculating the sample size for your research. In that case, you may still need to collect the data to compute the mean and standard deviation. For this calculation, you need an estimated value obtained from a pilot collection with few observations. These values can also be acquired from other studies with populations, species, or conditions similar to your research or even from theoretical models.

Now click  Calculate and transfer to main windows .  The estimated d value for your data will be calculated, and the Effect size d field will be filled in.

Finally, click on  Calculate , and voilà… Now you have the total sample size and those of groups 1 and 2!

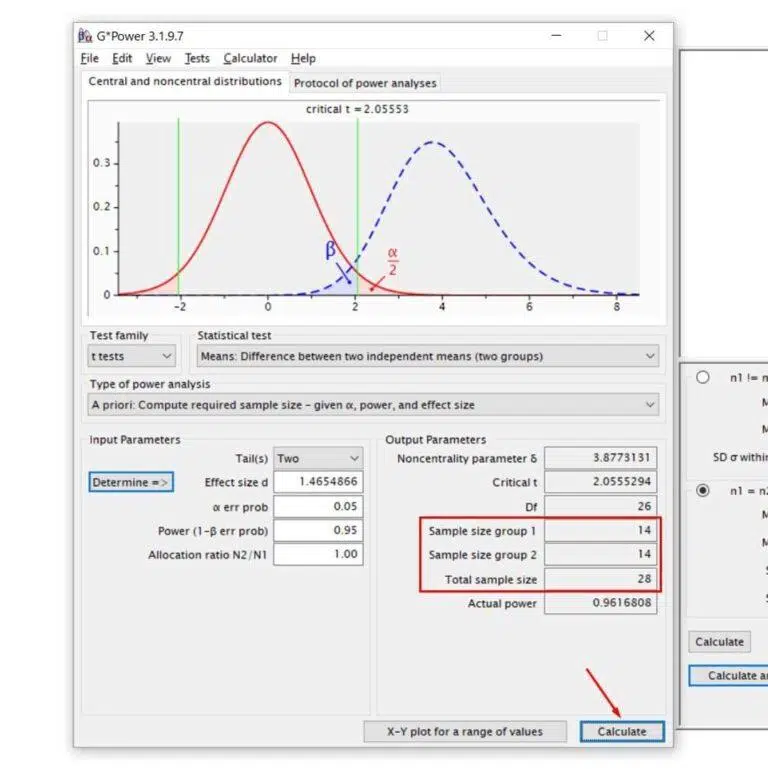
To calculate the sample size for the dependent samples t-test, click the  Tests: Means: Two dependent groups (matched pairs)  tab.

Then fill in the data exactly as we learned for the independent samples t-test. The only difference is that now you need to enter a value for  Correlation between groups . Then, run a Pearson correlation between the two groups using the pilot collection data to obtain this value. Finally, fill in the obtained r-value.

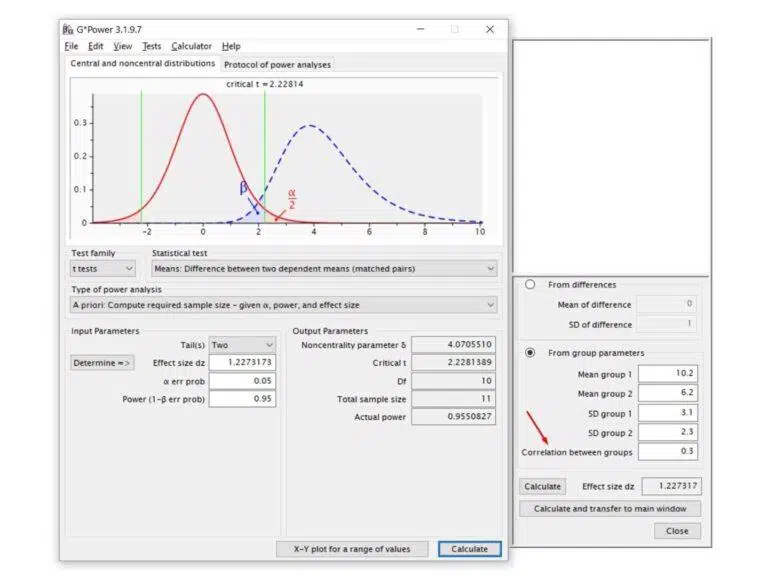
Concluding Remarks

Calculating the sample size for the t-test is a straightforward but essential step for obtaining more reliable results, saving time, and conserving resources. You’ll need some preliminary data concerning the two groups you’re comparing in the calculation. This data can come from a pilot collection, be compiled from other similar studies, or be theoretically estimated.

Do you feel prepared to discover the key to performing a flawless t-test now that you have learned how to determine its sample size? Read this article to find out: The Secrets of the t-Test .

Want to learn how to calculate sample size in G*Power for the most crucial inferential analyses?

Don’t miss out on the FREE samples of our recently launched digital book!

Inside, you’ll master sample size calculation for independent or paired t-tests; one- or two-way ANOVA, with or without repeated measures, and mixed models; simple and multiple linear and logistic regression , and more.

Click this link and discover everything it has to offer: Applied Statistics: Data Analysis .

Visit us on our social networks

DAILY POSTS ON INSTAGRAM!

sample size t-test

Similar posts.

Kruskal-Wallis Test: Mastering Non-Parametric Analysis for Multiple Groups

Unlock the potential of the Kruskal-Wallis Test for analyzing non-parametric data across multiple groups with precision and clarity.

What is the Difference Between the Sample and the Population?

Uncover the key differences between sample and population in statistics for accurate data interpretation and informed decision-making.

When The P-Value is Less Than 0.05: Understanding Statistical Significance

Discover the meaning of “when P value is less than 0.05,” its relevance to statistical significance, and how to interpret and understand its limitations.

Logistic Regression Using R: The Definitive Guide

This definitive guide unlocks the secrets of logistic regression using R—master predictive modeling for insightful data analysis.

What Are The 3 Types of Logistic Regression?

Discover the three types of logistic regression: Binary, Ordinal, and Multinomial. Understand their unique applications in statistical analysis and data science.

What is the Difference Between ANOVA and T-Test?

Learn the key differences between t-tests and ANOVA, when to use each, and avoid common errors. Explore more relevant articles on our blog.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Two Sample t-test: Definition, Formula, and Example

A two sample t-test is used to determine whether or not two population means are equal.

This tutorial explains the following:

• The motivation for performing a two sample t-test.
• The formula to perform a two sample t-test.
• The assumptions that should be met to perform a two sample t-test.
• An example of how to perform a two sample t-test.

Two Sample t-test: Motivation

Suppose we want to know whether or not the mean weight between two different species of turtles is equal. Since there are thousands of turtles in each population, it would be too time-consuming and costly to go around and weigh each individual turtle.

Instead, we might take a simple random sample of 15 turtles from each population and use the mean weight in each sample to determine if the mean weight is equal between the two populations:

However, it’s virtually guaranteed that the mean weight between the two samples will be at least a little different. The question is whether or not this difference is statistically significant . Fortunately, a two sample t-test allows us to answer this question.

Two Sample t-test: Formula

A two-sample t-test always uses the following null hypothesis:

• H 0 : μ 1  = μ 2 (the two population means are equal)

The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:

• H 1 (two-tailed): μ 1  ≠ μ 2 (the two population means are not equal)
• H 1 (left-tailed): μ 1  < μ 2  (population 1 mean is less than population 2 mean)
• H 1 (right-tailed):  μ 1 > μ 2  (population 1 mean is greater than population 2 mean)

We use the following formula to calculate the test statistic t:

Test statistic:  ( x 1  –  x 2 )  /  s p (√ 1/n 1  + 1/n 2 )

where  x 1  and  x 2 are the sample means, n 1 and n 2  are the sample sizes, and where s p is calculated as:

s p = √  (n 1 -1)s 1 2  +  (n 2 -1)s 2 2  /  (n 1 +n 2 -2)

where s 1 2  and s 2 2  are the sample variances.

If the p-value that corresponds to the test statistic t with (n 1 +n 2 -1) degrees of freedom is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis.

Two Sample t-test: Assumptions

For the results of a two sample t-test to be valid, the following assumptions should be met:

• The observations in one sample should be independent of the observations in the other sample.
• The data should be approximately normally distributed.
• The two samples should have approximately the same variance. If this assumption is not met, you should instead perform Welch’s t-test .
• The data in both samples was obtained using a random sampling method .

Two Sample t-test : Example

Suppose we want to know whether or not the mean weight between two different species of turtles is equal. To test this, will perform a two sample t-test at significance level α = 0.05 using the following steps:

Step 1: Gather the sample data.

Suppose we collect a random sample of turtles from each population with the following information:

• Sample size n 1 = 40
• Sample mean weight  x 1  = 300
• Sample standard deviation s 1 = 18.5
• Sample size n 2 = 38
• Sample mean weight  x 2  = 305
• Sample standard deviation s 2 = 16.7

Step 2: Define the hypotheses.

We will perform the two sample t-test with the following hypotheses:

• H 0 :  μ 1  = μ 2 (the two population means are equal)
• H 1 :  μ 1  ≠ μ 2 (the two population means are not equal)

Step 3: Calculate the test statistic  t .

First, we will calculate the pooled standard deviation s p :

s p = √  (n 1 -1)s 1 2  +  (n 2 -1)s 2 2  /  (n 1 +n 2 -2)  = √  (40-1)18.5 2  +  (38-1)16.7 2  /  (40+38-2)  = 17.647

Next, we will calculate the test statistic  t :

t = ( x 1  –  x 2 )  /  s p (√ 1/n 1  + 1/n 2 ) =  (300-305) / 17.647(√ 1/40 + 1/38 ) =  -1.2508

Step 4: Calculate the p-value of the test statistic  t .

According to the T Score to P Value Calculator , the p-value associated with t = -1.2508 and degrees of freedom = n 1 +n 2 -2 = 40+38-2 = 76 is  0.21484 .

Step 5: Draw a conclusion.

Since this p-value is not less than our significance level α = 0.05, we fail to reject the null hypothesis. We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.

Note:  You can also perform this entire two sample t-test by simply using the Two Sample t-test Calculator .

Additional Resources

The following tutorials explain how to perform a two-sample t-test using different statistical programs:

How to Perform a Two Sample t-test in Excel How to Perform a Two Sample t-test in SPSS How to Perform a Two Sample t-test in Stata How to Perform a Two Sample t-test in R How to Perform a Two Sample t-test in Python How to Perform a Two Sample t-test on a TI-84 Calculator

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “Two Sample t-test: Definition, Formula, and Example”

I like the detailed information and simplified in the way I can understand and relate easily. Thank you

It seems a couple of parenthesis is missed at the pooled standard deviation formula. Under square root you have (n1-1)s12 + (n2-1)s22 / (n1+n2-2) but it should be [(n1-1)s12 + (n2-1)s22] / (n1+n2-2) I used square bracket

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.