5 problem solving strategies for math

5 Strategies for Successful Problem Solving

• Powerful teaching strategies
• December 26, 2023
• Michaela Epstein

Blog > 5 Strategies for Successful Problem Solving

Problem solving can change the way students see maths – and how they see themselves as maths learners.

But, it's tough to help all students get the most out of a task.

To help, here are  5 Strategies for Problem Solving Success.

These are 5 valuable lessons I've learned from working with teachers across the globe .  You can use these strategies with all your students, no matter their level.

5 Strategies for Problem Solving Success

Your own enthusiasm is quickly picked up by your students. So, choose a problem, puzzle or game that you’re excited and curious about.

How do you know what will spark your curiosity? Do the task yourself!

(That’s why,  in the workshops I run , we spend a lot of time  actually  exploring problems. It’s a chance to step into students' shoes and experience maths from their perspective.)

Often, curriculum content becomes the goal of problem solving. For example, adding fractions, calculating areas or solving quadratic equations.

But, this is a mistake! Here's why-

Low floor, high ceiling tasks give students choices. Choices about what strategies to use, tools to draw on – and even what end-points to get to.

The most valuable goals focus on building confidence and capability in problem solving. For example:

• To make and break conjectures
• To use and evaluate different strategies
• To organise data in meaningful ways
• To explain and justify their conclusions.

The start of a task is what will get your students curious and hungry to get underway.

Consider: What's the least information your students will need?

At  ​our Members' online PL sessions​ , we look at one of four possibilities for launching a problem:

• Present a mystery to explore
• Present an example and non-example
• Run a demonstration game
• Show how to use a tool.

Keep the launch short – under 5 minutes. This is just enough to keep students’ attention AND share essential information.

Let’s face it, problem solving is hard, no matter your age or mathematical skill set.

Students aren’t afraid of hard work – they’re afraid of feeling or looking stupid. And, when those tricky maths moments do come, you can help.

Using questions, tools and other prompts can bring clarity and boost confidence.

(Here's a  free question catalogue  you might find handy to have in your back pocket.)

This careful support will help your students find problem solving far less daunting. Instead, it can become a chance for wonderous mathematical exploration.

Picture this: Your students are elbows deep in a problem, there’s a buzz in the air – oh, and only a minute until the bell.

The  most important  stage of a problem solving task – right at the end – is often the one that gets dropped off.

Why does ‘wrapping up’ matter?

In the last 10 minutes of a problem, students can share conjectures, strategies and solutions. It's also a chance to consider new questions that may open up further exploration.

In wrapping up, important learning will happen. Your students will observe patterns, make connections and clarify conjectures. You might even notice ‘aha’ moments.

Five strategies for problem solving success:

• Choose a task that YOU'RE keen on,
• Set a goal for strengthening problem solving skills,
• Plan a short launch to make the task widely accessible,
• Use questions, tools and prompts to support productive exploration, and
• Wrap up to create space for pivotal learning.

Join the Conversation

Dear Michaela, Greetings !! Thank you for sharing the strategies for problem solving task. These strategies will definitely enhance the skill in the mindset of young learners. In India ,Students of Grade 9 and Grade 10 have to learn and solve lot of theorems of triangle, Quadrilateral, Circle etc. Being an educator I have noticed that most of the students learn the theorems and it’s derivation by heart as a result they lack in understanding the application of these theorems.

I will appreciate if you can share your insights as how to make these topics interesting and easy to grasp.

Once again thanks for sharing such informative ideas.

Leave a comment

Cancel reply.

Your email address will not be published. Required fields are marked *

Don’t miss a thing!

Sign up to our mailing list for inspiring maths teaching ideas, event updates, free resources, and more!

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE :

• 8 Common Core math examples
• Tier 3 Interventions: A School Leaders Guide
• Tier 2 Interventions: A School Leaders Guide
• Tier 1 Interventions: A School Leaders Guide

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies for problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

How To Teach Math: 10 Effective Strategies For Teaching Math In The Classroom

Building Thinking Classrooms: Effective Strategies For Your Math Classroom

Differentiation Strategies In The Classroom: 8 Methods For Every Teacher

Retrieval Practice: A Foolproof Method To Improve Student Retention and Recall

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

The 5 Best Strategies for Solving Math Word Problems

As a math teacher with years of experience teaching word problems and problem-solving skills, I’ve seen how math word problems can spark both negative feelings and moments of triumph in students. 

There is something about applying math strategies to the real world in different ways that can shake the confidence of math students. All it takes is a few negative experiences with math word problems for a student to develop a life-long struggle with math.

That’s why I have put together this problem-solving strategy guide! My goal is to share my 5 best strategies for solving math word problems so that you can worry less about finding the correct solution and focus more on feeling confident when solving problems!

My 5 Best Strategies for Solving Math Word Problems

The key to problem solving lies in building a solid problem-solving process and equipping yourself with confidence in your use of math word problem strategies.

In my teaching experience , I’ve mastered breaking down complex problems into manageable steps in order to help students of all grade levels tackle everything from simple subtraction word problems to advanced algebraic equations. 

Below are my five best practices that not only help students find the correct answer but also build the confidence to approach different problems with a positive math mindset!

1. Understand the Problem by Focusing on Key Information

The first step in solving any mathematical problem is understanding the given problem. I always encourage students to read the problem carefully and identify key words and important information that provide clues about what the problem is asking.

One common mistake I see is that students often get distracted by extra information that isn’t necessary for solving the problem. The best way to avoid this is to underline key information and rewrite the question as a complete sentence in your own words.

Example Problem

“A group of 15 people are at a concert. They share 240 square feet of space while carrying 6 backpacks and 3 water bottles. If there are 10 people standing in a section of the space, how much space does each person in that section have?”

• Highlight the given information : 240 total square feet, 10 people in a section.
• Ignore extra information : The number of backpacks and water bottles isn’t necessary for solving the problem.
• Rewrite the question :  “How many square feet does each person in the section have?”

By focusing on only the key information and rewriting the problem in a simpler way, students can focus on solving the problem without being distracted by irrelevant details.

2. Break Down the Problem into Manageable Parts

Many math problems, especially complex problems, involve multiple steps.

The second strategy for solving math word problems that I always teach my students is to separate the task into different parts of the problem. This helps make a complex process more manageable.

For example, I often encourage my students to use a math model to start setting up the problem. I also encourage them to reflect on how each previous step connects to the next step of the problem-solving process.

“Find three consecutive integers whose sum is 72.”

We can start by defining the unknown number as x. This tells us that our the next number would be x+1, and the third would be x+2. This math model helps us understand how to proceed to the next step of the solution.

We can then write a math equation : \(x + (x + 1) + (x + 2) = 72\) that can be solved. We solve the equation step by step by first combining like terms.

\[3x + 3 = 72\]

We then use algebra to solve this simple two-step equation .

\[\begin{split} 3x + 3 – 3 & = 72 – 3 \\ \\ 3x &= 69 \\ \\ x&=23 \end{split}\]

This model helps students identify that algebra is the most appropriate strategy to determine the solution to the problem.

3. Use Visual and Logical Reasoning

Using visual representations of math concepts like counters, a task card, or fact families can make even the trickiest math word problems feel approachable.

When teaching mathematical word problems, I always encourage my students to use visual representations, regardless of whether they are in 3rd grade or older kids in high school.

Younger elementary school students might prefer using hands on manipulatives to solve multiplication problems or division word problems for example. High school students might prefer just sticking with drawing a diagram to represent all of the key information visually.

​ “A farmer has a rectangular garden that measures 30 feet in length and 20 feet in width. She wants to divide it into equal sections, each with an area of 100 square feet, for planting vegetables. How many sections can she create?”

• Solve : Divide the total area by the size of each section: 600 ÷ 100 = 6 sections.
• Draw a diagram : Sketch a rectangle to represent the garden. Label the dimensions (30 feet by 20 feet) and divide the rectangle into smaller sections, each labeled as 100 square feet.
• Highlight the key information visually : Use the total area of the garden (30 × 20 = 600 square feet) and the size of each section (100 square feet) to solve the problem.

Visualizing the problem with a diagram helps students understand the relationship between the total area, the size of each section, and the division process to find the number of sections.

This strategy works well for 3rd-grade students learning multiplication and division concepts and for older students tackling area-related problems.

4. Relate to Similar Problems and Real-World Scenarios

Relating different problems to similar problems students have already solved strengthens their understanding. This helps reinforce how an easy problem can provide strategies for tackling a different problem type that might be more difficult.

For example, if students know how to solve a division problem, such as sharing 12 candies among 4 kids, they can apply the same strategy to calculate portions for a group of people at a restaurant.

5. Review and Reflect on the Answer

The final step in my problem-solving process is reviewing the solution to ensure it matches the original problem. I make sure that I teach students to:

• Check their solution against the given information for accuracy.
• Substitute their final answer back into the equation to verify that it is the correct solution.
• Reflect on any mistakes made to avoid them in future problems.

“A rectangle’s perimeter is 36 meters. If the length is 10 meters, what is the width?”

We can solve this problem by using the perimeter formula: \(P=2L+2W\).

Substituting our known values results in: \(36=2(10)+2W\). We can simplify this to:

\[36=20+2W\]

We then use algebra to solve for the value of \(W\):

\[\begin{split} 36&=20+2W \\ 16 &= 2W \\ W&=8 \end{split}\]

We can then substitute to check our answer. We confirm that the width of 8 metres is the actual answer by revisiting the original problem. Substituting 8 in for W will show that we do in fact get a perimeter of 36 metres.

\[\begin{split} P&=2(10)+2(8) \\ &=20+16 \\ &=36 \end{split}\]

Since the calculated perimeter matches the original problem, we can confirm the solution.

This final reflection step helps foster a positive mindset and a deeper understanding of problem-solving strategies.

Applying Strategies for Solving Math Word Problems

Solving math word problems is a new skill that can initially seem overwhelming, but with consistent practice and the right strategies, you can tackle even the most complex problems with confidence and more positive thoughts. 

By focusing on key information, breaking down the problem, using visual aids, connecting to real-world examples, and reflecting on your solutions, you can improve your approach to any problem, whether you’re in 1st grade or beyond.

The more you practice these strategies, the more natural problem-solving will become. As you continue to apply these methods, you’ll not only improve your math skills but also build the confidence to handle problems in everyday situations. 

Keep practicing, and you’ll see your ability to solve math word problems grow with each challenge!

Did you find these strategies for solving math word problems helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!

RECOMMENDED FOR YOU

Here’s How to Do Math Word Problems the Easy Way!

20 Examples of Algebra in Everyday Life We Can All Relate To

• PRINT TO PLAY
• DIGITAL GAMES

Problem-Solving Strategies

October 16, 2019

There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.

Problem-solving strategies

1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.

Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.

Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?

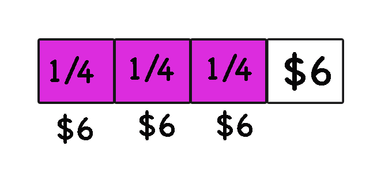
2. Guess and check

Teach students the same strategy research mathematicians use.

With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly.  By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.

Find two numbers that have sum 11 and product 24.

Try/guess  5 and 6  the product is 30 too high

  adjust  to 4 and 7 with product 28 still high

  adjust  again 3 and 8 product 24

3. Make a table or a list

Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.

To make sure you are listing all the information correctly read the problem carefully.

Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.

Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?

A table or list is useful in solving logic problems.

Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.

Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.

Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.

5. Find a pattern.

Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.

 The “rule” can then be used to find the answer to the question and complete the table/list.

Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?

6. Working backward

Problems that can be solved with this strategy are the ones that  list a series of events or a sequence of steps .

In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.

Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.

For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.

The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.

8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took

8+31+5+4= 48   Answer: The box came with 48 pieces of candy.

Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.

Print and digital activities

I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.

sample below

How to use the activity cards

Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.

Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.

For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.

Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.

Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions

There are 2 versions of the resource

70 google slides with explanations + 70 printable task cards

70 google slides with explanations + 11 worksheets

You might also like

Multiplying fractions/mixed numbers/simplifying

Adding and subtracting fractions

AM/PM, 24-hour clock, Elapsed Time – ideas, games, and activities

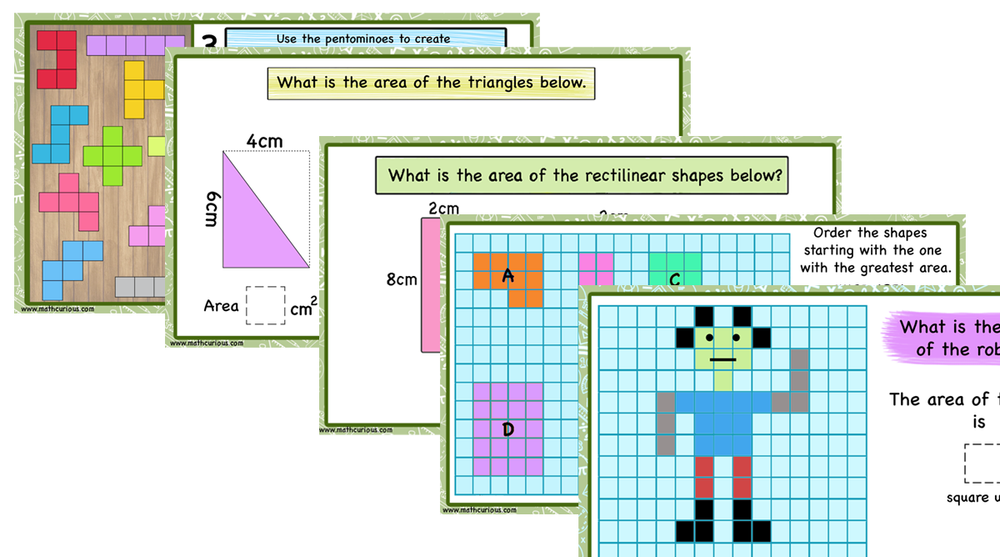
Teaching area, ideas, games, print, and digital activities

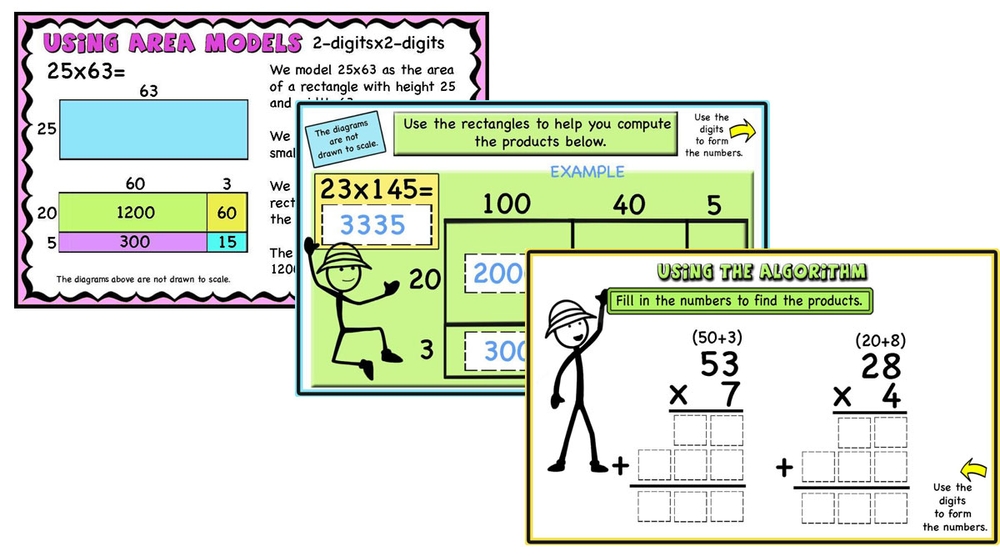
Multi-Digit Multiplication, Area model, Partial Products algorithm, Puzzles, Word problems

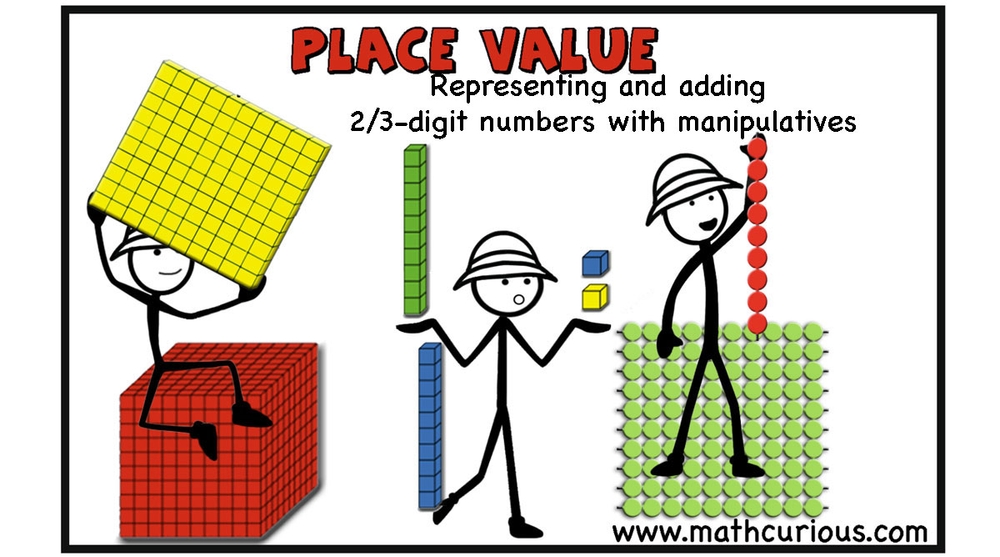
Place Value – Representing and adding 2/3 digit numbers with manipulatives

Multiplication Mission – arrays, properties, multiples, factors, division

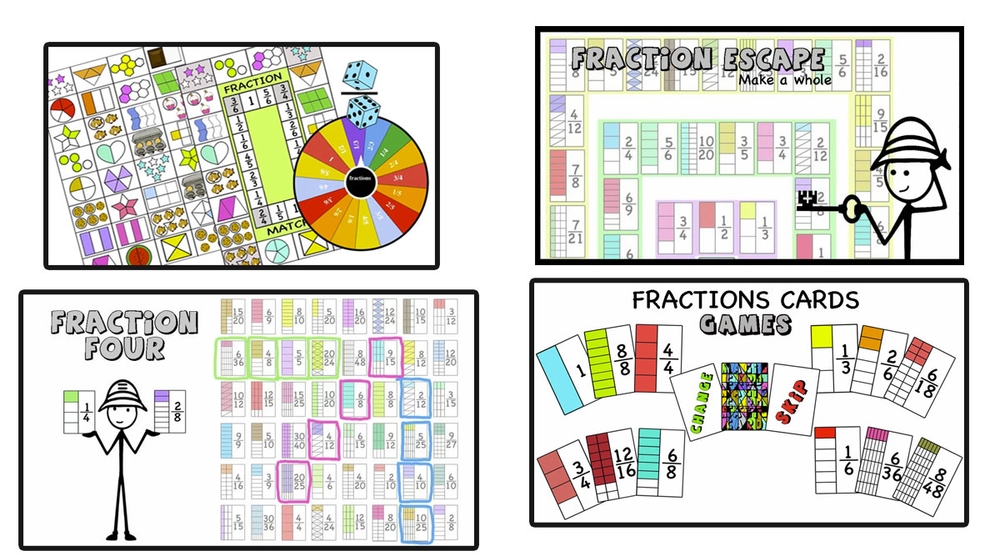
Fractions Games and activities – Equivalence, make 1, compare, add, subtract, like, unlike

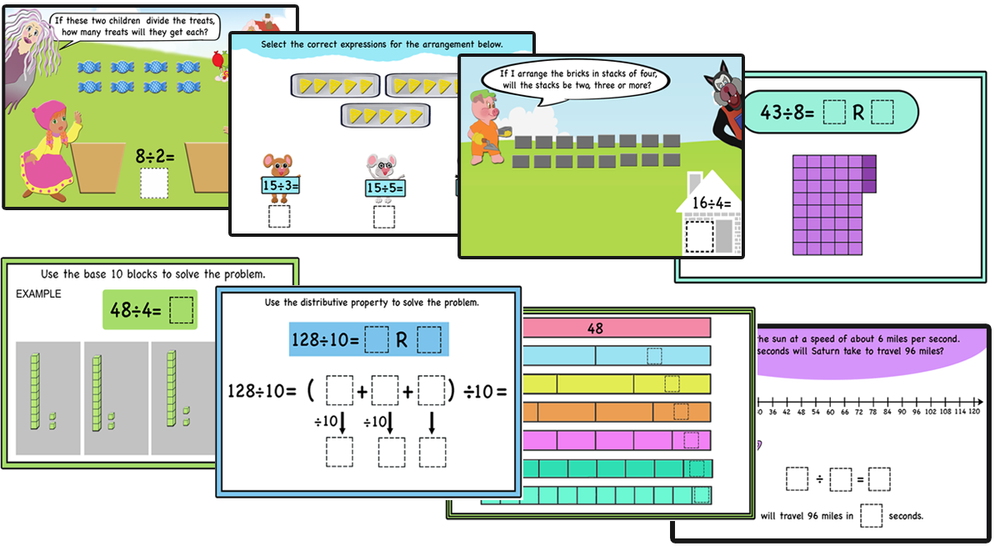
Diving into Division -Teaching division conceptually

Expressions with arrays

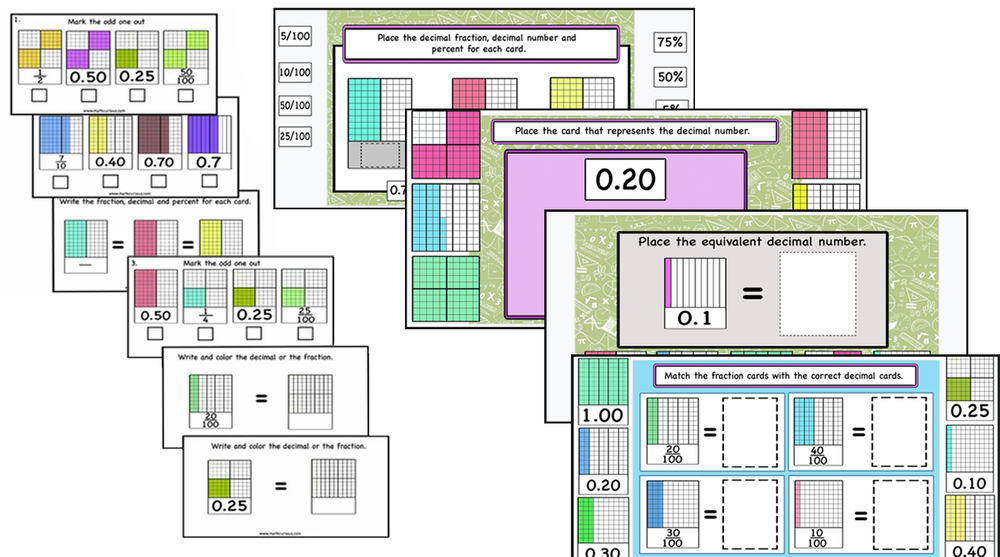
Decimals, Decimal fractions, Percentages – print and digital

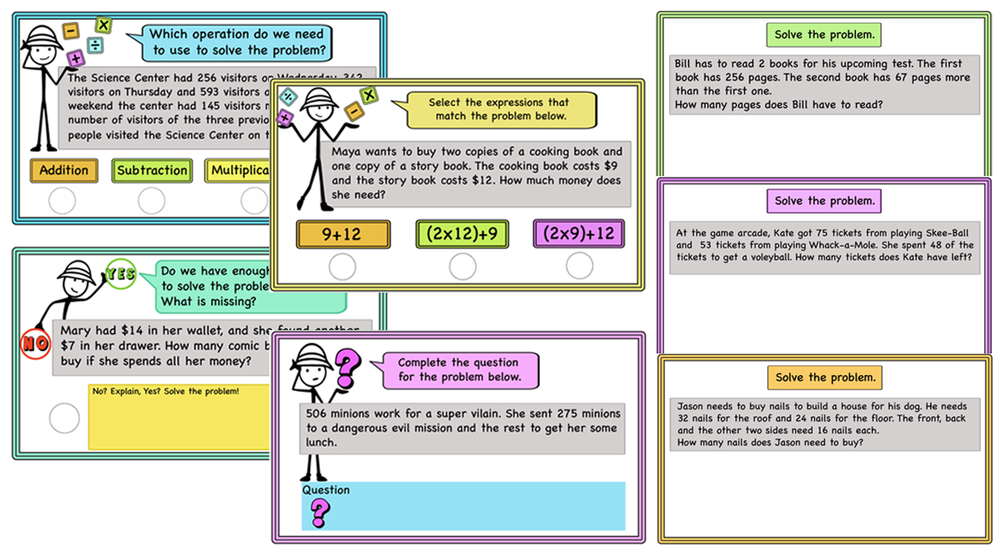
Solving Word Problems- Math talks-Strategies, Ideas and Activities-print and digital

Check out our best selling card games now available at amazon.com and amazon.ca.

Chicken Escape

A multiplayer card game that makes mental math practice fun! Chicken Escape is a fast-paced multiplayer card game. While playing…

Dragon Times – A math Adventure card game

Dragon Times is an educational fantasy card game that aims to motivate children to practice multiplication and division facts while…

5 Essential Problem Solving Techniques

• Critical Thinking

In the first post in this series, I talked about the difference between solving problems and problem solving. This week, I will continue my series on problem solving and share five essential problem solving techniques for your problem solving routines.

A strong problem-solving routine is essential for helping students develop their problem-solving strategy toolboxes. Over the years, I have used a variety of routines that have helped my students develop problem-solving strategies and critical thinking skills. (Read more about my favorite routine here !) Through a lot of trial and error, I found several routines that worked well for my students. (I will share more about them next week!) Today, I want to share some trade secrets with you to help you get the most from your problem-solving routines with five essential problem-solving techniques.

Five Essential Problem Solving Techniques

1. share student thinking and strategies..

This is essential! I can’t tell you how many times I have seen teachers give a great problem solving or critical thinking task and then never allow students to share their responses. Sometimes, our students are the best teachers and they can get a message across when we struggle to do so. Also, providing an opportunity for students to talk to other students about their thinking increases math vocabulary and builds communication skills.

After students have had an opportunity to share their thinking with a group member or partner, I encourage you to discuss the task as a class. This gives the teacher an opportunity to reiterate correct thinking, modify incorrect thinking, ask questions, build math vocabulary, and increase students’ communication skills.

Read more about getting started with math talk in the classroom here .

2. Solve non-routine problems.

In an earlier blog post, I emphasized the importance of using non-routine problems with students. Not only are students typically more engaged, but students have the opportunity to use strategies beyond writing an equation/number sentence or drawing a picture. If you’re interested in some fun, non-routine tasks, please check out my Solve It! Friday page.

One of the things many people say they love about math is the fact that there is a right and wrong answer. While there certainly are wrong answers, sometimes, there can be more than one right answer. These types of tasks really stretch some kids’ thinking. They also provide a natural venue for discussion. Students can debate the answers only to discover that more than one works!

3. Discuss efficiency.

During problem-solving experiences, students will often use beautiful and complicated solution strategies to solve problems. While we want to encourage outside-of-the-box thinking, we also want students to attend to efficiency. One way to do this is to have several students share their solutions. They can then discuss what strategies are best for specific types of problems. When discussing difficulty becomes a regular part of your routine, students will begin to utilize their problem-solving strategies in a way that not only gets them to the correct answer but also using an efficient method.

4. Make connections.

Recently, I wrote about making connections as part of my Summer PD series. Read it here ! When students make connects, it deepens their understanding of other content and skills. One way to do this is to connect the problem-solving task to grade-level content and skills. Another way is to have students represent problems in a variety of ways, i.e. pictures, numbers, words, or equations. Each representation is crafted in a specific way, so being able to translate words into an equation or numbers into a picture is a big skill that has many benefits.

5. Use “high ceiling, low floor tasks.”

The term “high ceiling, low floor” refers to a task having multiple entry points to allow all students a way to access the task; however, it also includes ways to extend the tasks for those students who are ready for more of a challenge. These types of tasks increase participation because students can participate at a level that is comfortable for them. Students are also able to showcase what they can do instead of what they are unable to do. Even better, these tasks provide instant opportunities for differentiation because all students can participate in a way that allows them to be most successful.

Using a regular problem-solving routine can help students develop the tools necessary to be powerful thinkers of mathematics; however, in order to get the most from the routines, certain problem-solving techniques must be included. While you may not want to add all of the above techniques to your routine, I encourage you to commit to adding one or two of them this year. I highly recommended starting with “sharing student thinking and strategies.” It’s probably the most important technique of all of the problem-solving routines. It will get you the most bang for your buck!

Sound Off! How do get the most from your problem-solving routine? Which problem-solving techniques do you think are most important?

Shametria Routt Banks

• Assessment Tools
• Content and Standards
• Differentiation
• Math & Literature
• Math & Technology
• Math Routines
• Math Stations
• Virtual Learning
• Writing in Math

You may also like...

3 Responses

Hi, can you provide an example of a high ceiling, low floor task? Thank you!

Hi Jen! Great question! The high ceiling, low floor tasks give all students a chance to engage in the task but have places to go to extend the learning for students. One problem that comes to mind is a task where students are asked to find combinations of numbers to achieve a goal, like the following problem: Farmer Brown’s niece Angie is in charge of her uncle’s farm while he is on vacation. He gave her strict instructions to make sure none of the animals ran away. When Angie counted the pigs and chickens, she counted 32 legs. How many pigs and chickens did she count? All students should be able to determine a combination of pigs and chickens; however, what if I added a new condition to say: Angie counted a total of 12 animals. This changes the level of rigor because students are now looking for a specific combination. Some students will struggle with this but others may be ready to tackle it; so, using tasks that have a high-ceiling allow for this flexibility. Check out more high ceiling, low floor tasks here: https://www.youcubed.org/task-grades/low-floor-high-ceiling/ .

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

©2024 The Routty Math Teacher.   All Rights Reserved.  Designed by Ashley Hughes.

Privacy overview, grade level.

You are using an outdated browser. Please upgrade your browser to improve your experience.

Math Problem Solving Strategies That Make Students Say “I Get It!”

Even students who are quick with math facts can get stuck when it comes to problem solving.

As soon as a concept is translated to a word problem, or a simple mathematical sentence contains an unknown, they’re stumped.

That’s because problem solving requires us to  consciously choose the strategies most appropriate for the problem   at hand . And not all students have this metacognitive ability.

But you can teach these strategies for problem solving.  You just need to know what they are.

We’ve compiled them here divided into four categories:

Strategies for understanding a problem

Strategies for solving the problem, strategies for working out, strategies for checking the solution.

Get to know these strategies and then model them explicitly to your students. Next time they dive into a rich problem, they’ll be filling up their working out paper faster than ever!

Before students can solve a problem, they need to know what it’s asking them. This is often the first hurdle with word problems that don’t specify a particular mathematical operation.

Encourage your students to:

Read and reread the question

They say they’ve read it, but have they  really ? Sometimes students will skip ahead as soon as they’ve noticed one familiar piece of information or give up trying to understand it if the problem doesn’t make sense at first glance.

Teach students to interpret a question by using self-monitoring strategies such as:

• Rereading a question more slowly if it doesn’t make sense the first time
• Asking for help
• Highlighting or underlining important pieces of information.

Identify important and extraneous information

John is collecting money for his friend Ari’s birthday. He starts with $5 of his own, then Marcus gives him another $5. How much does he have now?

As adults looking at the above problem, we can instantly look past the names and the birthday scenario to see a simple addition problem. Students, however, can struggle to determine what’s relevant in the information that’s been given to them.

Teach students to sort and sift the information in a problem to find what’s relevant. A good way to do this is to have them swap out pieces of information to see if the solution changes. If changing names, items or scenarios has no impact on the end result, they’ll realize that it doesn’t need to be a point of focus while solving the problem.

Schema approach

This is a math intervention strategy that can make problem solving easier for all students, regardless of ability.

Compare different word problems of the same type and construct a formula, or mathematical sentence stem, that applies to them all. For example, a simple subtraction problems could be expressed as:

[Number/Quantity A] with [Number/Quantity B] removed becomes [end result].

This is the underlying procedure or  schema  students are being asked to use. Once they have a list of schema for different mathematical operations (addition, multiplication and so on), they can take turns to apply them to an unfamiliar word problem and see which one fits.

Struggling students often believe math is something you either do automatically or don’t do at all. But that’s not true. Help your students understand that they have a choice of problem-solving strategies to use, and if one doesn’t work, they can try another.

Here are four common strategies students can use for problem solving.

Visualizing

Visualizing an abstract problem often makes it easier to solve. Students could draw a picture or simply draw tally marks on a piece of working out paper.

Encourage visualization by modeling it on the whiteboard and providing graphic organizers that have space for students to draw before they write down the final number.

Guess and check

Show students how to make an educated guess and then plug this answer back into the original problem. If it doesn’t work, they can adjust their initial guess higher or lower accordingly.

Find a pattern

To find patterns, show students how to extract and list all the relevant facts in a problem so they can be easily compared. If they find a pattern, they’ll be able to locate the missing piece of information.

Work backward

Working backward is useful if students are tasked with finding an unknown number in a problem or mathematical sentence. For example, if the problem is 8 + x = 12, students can find x by:

• Starting with 12
• Taking the 8 from the 12
• Being left with 4
• Checking that 4 works when used instead of x

Now students have understood the problem and formulated a strategy, it’s time to put it into practice. But if they just launch in and do it, they might make it harder for themselves. Show them how to work through a problem effectively by:

Documenting working out

Model the process of writing down every step you take to complete a math problem and provide working out paper when students are solving a problem. This will allow students to keep track of their thoughts and pick up errors before they reach a final solution.

Check along the way

Checking work as you go is another crucial self-monitoring strategy for math learners. Model it to them with think aloud questions such as:

• Does that last step look right?
• Does this follow on from the step I took before?
• Have I done any ‘smaller’ sums within the bigger problem that need checking?

Students often make the mistake of thinking that speed is everything in math — so they’ll rush to get an answer down and move on without checking.

But checking is important too. It allows them to pinpoint areas of difficulty as they come up, and it enables them to tackle more complex problems that require multiple checks  before  arriving at a final answer.

Here are some checking strategies you can promote:

Check with a partner

Comparing answers with a peer leads is a more reflective process than just receiving a tick from the teacher. If students have two different answers, encourage them to talk about how they arrived at them and compare working out methods. They’ll figure out exactly where they went wrong, and what they got right.

Reread the problem with your solution

Most of the time, students will be able to tell whether or not their answer is correct by putting it back into the initial problem. If it doesn’t work or it just ‘looks wrong’, it’s time to go back and fix it up.

Fixing mistakes

Show students how to backtrack through their working out to find the exact point where they made a mistake. Emphasize that they can’t do this if they haven’t written down everything in the first place — so a single answer with no working out isn’t as impressive as they might think!

Need more help developing problem solving skills?

Read up on  how to set a problem solving and reasoning activity  or explore Mathseeds and Mathletics, our award winning online math programs. They’ve got over 900 teacher tested problem solving activities between them!

Get access to 900+ unique problem solving activities

You might like....

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

• What do you know?
• What do you need to know?
• Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

• Identify - What is the question?
• Plan - What strategy will I use to solve the problem?
• Solve - Carry out your plan.
• Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square.   18 + 2 = 20   If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square   61 + (3 x 7) = 82   If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

The following are some other examples of problem solving strategies.

Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)

Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.